某校校庆，各届校友纷至沓来，某班共来了n位校友(n>8且n∈N*)，其中女校友6位，组委会对这n位校友登记制作了一份校友名单，现随机从中选出2位校友代表，若选出的2位校友是一男一女，则称为“最佳组合”．
(1)若随机选出的2位校友代表为“最佳组合”的概率不小于
，求n的最大值；
(2)当n＝12时，设选出的2位校友代表中女校友人数为ξ，求ξ的分布列和数学期望E(ξ)．
（本小题满分14分）
已知各项均不相等的等差数列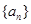
的前四项和为14，且
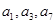恰为等比数列
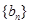的前三项。
（1）分别求数列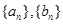
的前n项和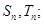
（2）设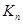
为数列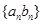
的前n项和，若不等式
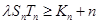对一切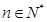
恒成立，求实数
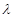的最小值。
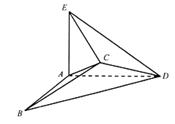
如图，将边长为2的正方形ABCD沿对角线BD折成一个直二面角，且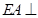
平面ABD，AE=a。
（1）若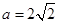
，求证：AB//平面CDE；
（2）求实数a的值，使得二面角A—EC—D的大小为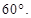
已知函数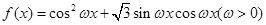
的最小正周期为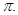
（1）求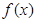
的单调递增区间；
（2）在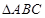
中，a、b、c分别是角A、B、C的对边，若
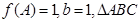的面积为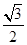
，求a的值。
（本小题满分15分）
已知抛物线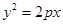
上任一点到焦点的距离比到y轴距离大1。
（1）求抛物线的方程；
（2）设A，B为抛物线上两点，且AB不与x轴垂直，若线段AB的垂直平分线恰过点M（4，0），求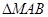
的面积的最大值。
（本小题满分15分）
已知函数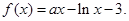
（1）当a=1时，求函数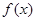
在点（1，-2）处的切线方程；
（2）若函数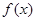在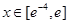
上的图象与直线
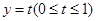总有两个不同交点，求实数a的取值范围。