(本小题满分15分)
已知函数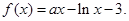
(1)当a=1时,求函数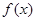 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;
(2)若函数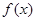 在
在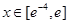 上的图象与直线
上的图象与直线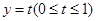 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。
近期世界各国军事演习频繁,某国一次军事演习中,空军同时出动了甲、乙、丙三架不同型号的战斗机对一目标进行轰炸,已知甲击中目标的概率是 ;甲、丙同时轰炸一次,目标未被击中的概率是
;甲、丙同时轰炸一次,目标未被击中的概率是 ;乙、丙同时轰炸一次都击中目标的概率是
;乙、丙同时轰炸一次都击中目标的概率是 .
.
(Ⅰ)求乙、丙各自击中目标的概率.(Ⅱ)求目标被击中的概率.
(本小题满分12分)在平面直角坐标系 中,已知圆
中,已知圆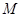 过坐标原点
过坐标原点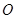 且圆心在曲线
且圆心在曲线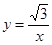 上.
上.
(Ⅰ)若圆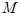 分别与
分别与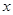 轴、
轴、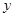 轴交于点
轴交于点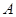 、
、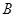 (不同于原点
(不同于原点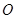 ),求证:
),求证: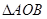 的面积为定值;
的面积为定值;
(Ⅱ)设直线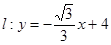 与圆
与圆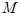 交于不同的两点
交于不同的两点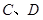 ,且
,且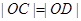 ,求圆
,求圆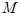 的方程;
的方程;
(Ⅲ)设直线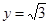 与(Ⅱ)中所求圆
与(Ⅱ)中所求圆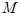 交于点
交于点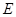 、
、 ,
, 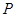 为直线
为直线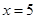 上的动点,直线
上的动点,直线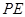 ,
,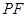 与圆
与圆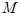 的另一个交点分别为
的另一个交点分别为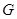 ,
, ,求证:直线
,求证:直线 过定点.
过定点.
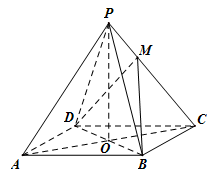
(本小题满分12分)如图,已知四棱锥 的底面是菱形,对角线
的底面是菱形,对角线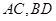 交于点
交于点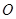 ,
,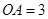 ,
,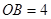 ,
,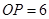 ,
,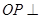 底面
底面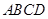 ,点满足
,点满足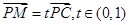 .
.
(1)当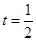 时,证明:
时,证明: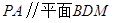 .
.
(2)若二面角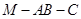 的大小为
的大小为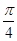 ,问:符合条件的点
,问:符合条件的点 是否存在.若存在,求出
是否存在.若存在,求出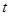 的值.若不存在,说明理由.
的值.若不存在,说明理由.
设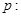 函数
函数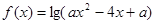 的值域为R;
的值域为R; 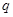 :不等式
:不等式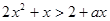 ,对
,对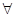
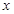 ∈(-∞,-1)上恒成立,如果命题“
∈(-∞,-1)上恒成立,如果命题“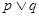 ”为真命题,命题“
”为真命题,命题“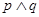 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知关于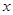 的二次函数
的二次函数
(Ⅰ)设集合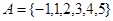 和
和 ,分别从集合
,分别从集合 ,
,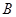 中随机取一个数作为
中随机取一个数作为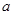 和
和 ,求函数
,求函数 在区间
在区间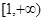 上是增函数的概率.
上是增函数的概率.
(Ⅱ)设点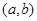 是区域
是区域 内的随机点,求函数
内的随机点,求函数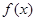 在区间
在区间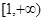 上是增函数的概率.
上是增函数的概率.