选修4-4:坐标系与参数方程
已知曲线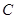 的参数方程为
的参数方程为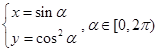 ,曲线
,曲线 的极坐标方程为
的极坐标方程为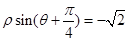 .
.
(1)将曲线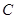 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)曲线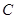 与曲线
与曲线 有无公共点?试说明理由.
有无公共点?试说明理由.
设函数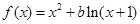 ,其中
,其中 .
.
(Ⅰ)当 时,判断函数
时,判断函数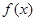 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)求函数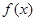 的极值点;
的极值点;
(Ⅲ)证明对任意的正整数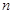 ,不等式
,不等式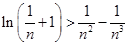 都成立.
都成立.
函数 ,过曲线
,过曲线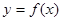 上的点
上的点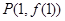 的切线方程为
的切线方程为 .
.
(1)若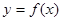 在
在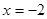 时有极值,求
时有极值,求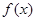 的表达式;
的表达式;
(2)在(1)的条件下,求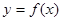 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(3)若函数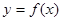 在区间[-2,1]上单调递增,求实数b的取值范围.
在区间[-2,1]上单调递增,求实数b的取值范围.
已知椭圆C:
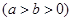 的离心率为
的离心率为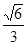 ,椭圆C上任意一点到椭圆两焦点的距离之和为6.
,椭圆C上任意一点到椭圆两焦点的距离之和为6.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线
与椭圆C交于A,B两点,点P(0,1),且满足PA=PB,求直线 的方程.
的方程.
已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为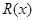 万元,且
万元,且
(1)写出年利润W(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
如图,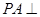 平面
平面 ,四边形
,四边形 是正方形,
是正方形,  ,点
,点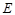 、
、 、
、 分别为线段
分别为线段 、
、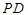 和
和 的中点.
的中点.
(1)求异面直线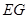 与
与 所成角的余弦值;
所成角的余弦值;
(2)在线段 上是否存在一点
上是否存在一点 ,使得点
,使得点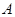 到平面
到平面 的距离恰为
的距离恰为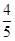 ?若存在,求出线段
?若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.