已知函数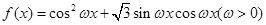 的最小正周期为
的最小正周期为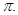
(1)求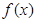 的单调递增区间;
的单调递增区间;
(2)在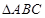 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若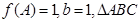 的面积为
的面积为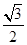 ,求a的值。
,求a的值。
养路处建造无底的圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米。养路处拟另建一个更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来增加4米(高不变);二是高度增加4米(底面直径不变)。
分别计算按这两种方案所建的仓库的体积;
分别计算按这两种方案所建的仓库的表面积;
哪个方案更经济些?
如图,在矩形ABCD中,已知AB=3, AD=1, E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: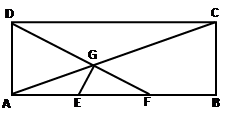
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G ⊥D F。
已知三角形ABC的顶点坐标分别为A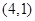 ,B
,B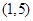 ,C
,C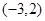 ;
;
(1)求直线AB方程的一般式;
(2)证明△ABC为直角三角形;
(3)求△ABC外接圆方程。
设数列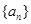 前n项和
前n项和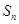 ,且
,且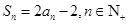 .
.
(Ⅰ)试求数列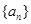 的通项公式;
的通项公式;
(Ⅱ)设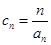 ,求数列
,求数列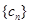 的前
的前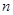 项和
项和
如图所示,现有 四个海岛,已知
四个海岛,已知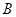 在
在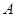 的正北方向
的正北方向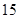 海里处,
海里处, 在
在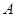 的东偏北30°方向,又在
的东偏北30°方向,又在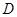 的东偏北45°方向,且
的东偏北45°方向,且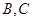 相距
相距 海里,求
海里,求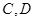 两岛间的距离.
两岛间的距离.