【2015高考重庆,理20】 设函数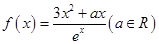
(1)若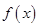 在
在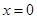 处取得极值,确定
处取得极值,确定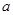 的值,并求此时曲线
的值,并求此时曲线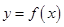 在点
在点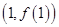 处的切线方程;
处的切线方程;
(2)若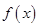 在
在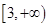 上为减函数,求
上为减函数,求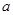 的取值范围。
的取值范围。
(本小题满分10分)选修4-4:坐标系与参数方程
已知圆锥曲线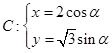 (
(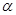 为参数)和定点
为参数)和定点 ,
,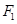 、
、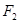 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点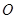 为极点,以
为极点,以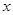 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线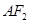 的直角坐标方程;
的直角坐标方程;
(2)经过点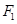 且与直线
且与直线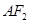 垂直的直线
垂直的直线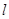 交此圆锥曲线于
交此圆锥曲线于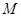 、
、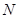 两点,求
两点,求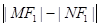 的值.
的值.
如图,在 中,
中, 是
是 的角平分线,
的角平分线, 的外接圆交
的外接圆交 于点
于点 ,
,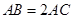 .
.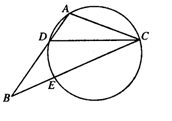
(Ⅰ)求证: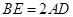 ;
;
(Ⅱ)当 ,
,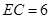 时,求
时,求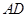 的长.
的长.
(本小题满分12分)已知函数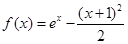 ,
, .
.
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ)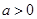 ,若
,若 ,求a的取值范围.
,求a的取值范围.
已知椭圆 的上顶点为
的上顶点为 ,直线
,直线 交椭圆于
交椭圆于 两点,设直线
两点,设直线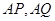 的斜率分别为
的斜率分别为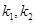 .
.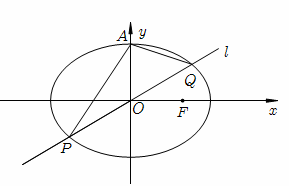
(1)若 时,求
时,求 的值;
的值;
(2)若 时,证明直线
时,证明直线 过定点.
过定点.
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量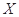 ,求
,求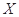 的分布列和数学期望
的分布列和数学期望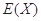 .
.