如图所示，建筑工地常用的一种“深穴打夯机”工作时，电动机带动两个紧压夯杆的滚轮匀速转动将夯从深为h的坑中提到地面，两个滚轮彼此分开，夯杆被释放，最后夯在自身重力作用下，落回深坑，夯实坑底，然后，两个滚轮再次压紧夯杆，夯再次被提到地面，如此周而复始。已知两个滚轮的半径R=0．2m，转动的角速度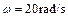
，每个滚轮对夯杆的正压力
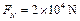，滚轮与夯杆间的动摩擦因数
，夯的总质量
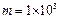kg，坑深h=6．4m，假定在打夯的过程中每次坑的深度变化不大，当夯的底端升到坑口时，滚轮将夯杆释放，不计空气阻力，取g=10m/s2，求：
（1）夯杆被滚轮压紧加速上升至与滚轮速度相等时，此时夯的底端离坑底的高度h1；
（2）夯的运动周期T；
（3）每个周期中，提升夯的过程中电动机所做的功W．
将1molCO和1molH2O充入某固定容积的反应器中，在某条件下达到平衡：
CO+H2O（g）
CO2+H2，此时有2/3的CO转化为CO2。
（1）该平衡混合物中CO2的体积分数为
（2）若容器体积为1L,到达平衡所需时间为2分钟，则H2的平均反应速率为
（3）若在相同条件下，向容器中充入1molCO2、1molH2和1molH2O，则达到平衡时与⑴中平衡相比较，平衡应向 （填“正反应方向”、“逆反应方向”或“不”）移动，此时平衡混合物中CO2的体积分数可能是下列各值中的
| A．22．2% | B．27．55% | C．33．3% | D．36．8% |
（4）结合（3）中计算结果分析若平衡向正方向移动时，则下列说法中正确的是（ ）
①生成物的产量一定增加； ②生成物的体积分数一定增加；
③反应物的转化率一定增大； ④反应物的浓度一定降低；
⑤正反应速率一定大于逆反应速率； ⑥一定使用了催化剂．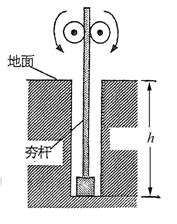
汽车刹车前的速度为5m/s，刹车获得的加速度大小为0.4m/s2.求：
（1）求汽车刹车开始后20s内滑行的距离
（2）求从开始刹车到汽车位移30m所经历的时间：
（3）静止前2.5s内汽车滑行的距离。
据报道,一儿童玩耍时不慎从45m高的阳台上无初速度落下,在他刚掉下时被楼下一社区管理人员发现,,该人员迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童,已知管理人员到楼底的距离为18m,为确保能稳稳接住儿童,不计空气阻力,忽略管理人员的反应时间, 取g=10m/s2,,问: 管理人员至少要用多大的平均速度跑到楼底?
汽车在高速公路上行驶的速度为108km/h，若驾驶员发现前方70m处发生了交通事故，马上紧急刹车，汽车以恒定的加速度经过4s才停下来，问该汽车是否会有安全问题？
细绳一端系着质量M=8kg的物体静止在水平面，另一端通过光滑小孔吊着质量m=2kg的物体，M的中点与圆孔的距离r=0.2m，已知M与水平面间的动摩擦因数为0.2，现使此物体M随转台绕中心轴转动，问转台角速度ω在什么范围m会处于静止状态？（设最大静摩擦力等于滑动摩擦力，g="10" m/s2）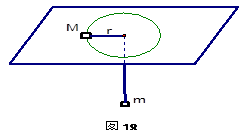
宇航员站在一星球表面上，沿水平方向以初速度v0从倾斜角为θ的斜面顶端P处抛出一个小球，测得经过时间t小球落在斜面上的另一点Q，已知该星球的半径为R，求：
（1）该星球表面的重力加速度。
（2）该星球的第一宇宙速度。