在“探究弹性势能的表达式”的活动中，为计算弹簧弹力所做功，把拉伸弹簧的过程分为很多小段，拉力在每小段可以认为是恒力，用各小段做功的代数和代表弹力在整个过程所做的功，物理学中把这种研究方法叫做“微元法”，下面几个实例中应用该方法的是（ ）
A．根据加速度的定义 ，当△t非常小， 就可以表示物体在某时刻的瞬时加速度 |
| B．在探究加速度、力和质量三者之间关系时，先保持质量不变研究加速度与力的关系，再保持力不变研究加速度与质量的关系 |
| C．在推导匀变速运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看作匀速直线运动，然后把各小段的位移相加 |
| D．在不需要考虑物体本身的大小和形状时，用点来代替物体，即质点 |
抖动绳子的一端，产生如图所示的横波，则绳上横波的波长为：( )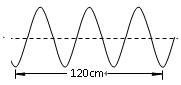
| A．120cm | B．80cm | C．40cm | D．20cm |
一列波从空气传入水中，保持不变的物理量是：（）
| A．波速 | B．波长 | C．频率 | D．振幅 |
下列关于波长的说法中，正确的是（）
| A．一个周期内媒质质点走过的路程 | B．横波中两个波峰间的距离 |
| C．一个周期内振动形式所传播的距离 | D．两个振动速度相同的媒质质点间的距离 |
弹簧振子在做简谐振动的过程中，振子通过平衡位置时 ( )
| A．速度值最大 | B．回复力的值最大 |
| C．加速度值最大 | D．位移最大 |
如图4所示“时空之旅”飞车表演时，演员驾着摩托车，在粗糙的球形金属网内壁上下盘旋，令人惊叹不已。摩托车沿图示竖直轨道做圆周运动的过程中，下列说法正确的是（）
| A．机械能一定守恒 |
| B．其输出功率始终保持恒定 |
| C．经过最低点的向心力仅由支持力提供 |
| D．通过最高点时的最小速度与球形金属网直径有关 |