如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0( ,-
,- ),角速度为1,那么点P到y轴距离d关于时间t的函数图像大致为 ( )
),角速度为1,那么点P到y轴距离d关于时间t的函数图像大致为 ( )

数列5,7,9,11, ,
, 的项数是( )
的项数是( )
A.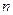 |
B.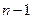 |
C. |
D. |
古希腊著名的毕达哥拉斯学派把1、3 、6、10……这样的数称为“三角形数”,而把1、4、9、16……这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式是
、6、10……这样的数称为“三角形数”,而把1、4、9、16……这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式是
①13=3+10;②25=9+16;③36=15+21;④49=18+31;⑤64="28+36" 
给出以下命题:⑴若 ,则f(x)>0; ⑵
,则f(x)>0; ⑵ ;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则 ;其中正确命题的个数为…
;其中正确命题的个数为…
| A.1 | B.2 | C.3 | D.0 |
已知 ,
, ,则
,则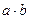 的取值范围为()
的取值范围为()
A. |
B.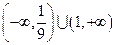 |
C. |
D.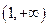 |
如图,在棱长均为2的正四棱锥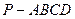 中,点E为PC的中点,则下列命题正确的是()(正四棱锥即底面为正方
中,点E为PC的中点,则下列命题正确的是()(正四棱锥即底面为正方 形,四条侧棱长相等,顶点在底面上的射影为底面的中心的四棱锥)
形,四条侧棱长相等,顶点在底面上的射影为底面的中心的四棱锥)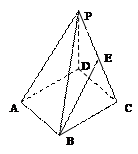
A.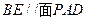 ,且直线BE到面PAD的距离为 ,且直线BE到面PAD的距离为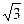 |
B.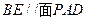 ,且直线BE到面PAD的距离为 ,且直线BE到面PAD的距离为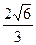 |
C.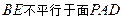 ,且直线BE与面PAD所成的角大于 ,且直线BE与面PAD所成的角大于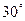 |
D.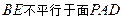 ,且直线BE与面PAD所成的角小于 ,且直线BE与面PAD所成的角小于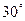 |