已知函数
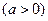 且导数
且导数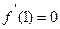 .
.
(Ⅰ)试用含有 的式子表示
的式子表示 ,并求
,并求 单调区间;(II)对于函数图象上的不同两点
单调区间;(II)对于函数图象上的不同两点 ,如果在函数图象上存在点
,如果在函数图象上存在点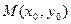 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称
,则称 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当 时,又称
时,又称 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数 上是否存在两点
上是否存在两点 、
、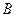 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出 、
、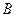 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知椭圆 的离心率为
的离心率为 ,点
,点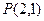 是椭圆上一定点,若斜率为
是椭圆上一定点,若斜率为 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点 、
、 .
.
(I)求椭圆方程;(II)求 面积的最大值.
面积的最大值.
已知菱形ABCD的边长为2,对角线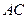 与
与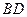 交于点
交于点 ,且
,且 ,M为BC的中点.将此菱形沿对角线BD折成二面角
,M为BC的中点.将此菱形沿对角线BD折成二面角 .
.
(I)求证:面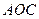
 面
面 ;(II)若二面角
;(II)若二面角 为
为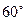 时,求直线
时,求直线 与面
与面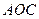 所成角的余弦值.
所成角的余弦值.
已知向量 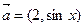 ,
, ,函数
,函数 .(Ⅰ)求
.(Ⅰ)求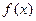 的单调增区间;(II)若在
的单调增区间;(II)若在 中,角
中,角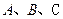 所对的边分别是
所对的边分别是 ,且满足:
,且满足: ,求
,求 的取值范围.
的取值范围.
一盒中装有分别标记着1,2,3,4数字的4个小球,每次从袋中取出一只球,设每只小球被取出的可能性相同.(I)若每次取出的球不放回盒中,现连续取三次球,求恰好第三次取出的球的标号为最大数字的球的概率;(II)若每次取出的球放回盒中,然后再取出一只球,现连续取三次球,这三次取出的球中标号最大数字为 ,求
,求 的概率分布列与期望.
的概率分布列与期望.