现有7名同学去参加一个活动,分别求出以下不同要求的方法数(以下各小题写出必要的计算公式,最终结果用数字作答)
(1)排队时7名同学中的丙不站在中间的排法
(2)排队时7名同学中的甲、乙、丙三名同学各不相邻的排法
(3)排队时7名同学中的甲不能站在最前并且已不能站在最后的排法(理科学生做)
(4)7名学生选出3名代表发言,甲,乙,丙三名同学至多两人个入选的选法(理科学生做)
7名学生中选出3名代表发言,甲、乙只有一人入选的选法有多少?(文科学生做)
观察下面一组组合数等式: ;
; ;
; ;
;
…………
(1)由以上规律,请写出第 个等式并证明;
个等式并证明;
(2)随机变量 ,求证:
,求证: .
.
正四面体 边长为2.
边长为2.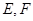 分别为
分别为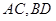 中点.
中点.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
在平面直角坐标系 中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1:
中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1: ,C2:
,C2: . 设点P的轨迹为
. 设点P的轨迹为 .
.
(1)求C的方程;
(2)设直线 与C交于A,B两点.问k为何值时
与C交于A,B两点.问k为何值时

 ?此时
?此时 的值是多少?
的值是多少?
已知数列 的前
的前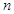 项和为
项和为 ,对一切正整数
,对一切正整数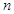 ,点
,点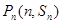 都在函数
都在函数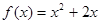 的图象上.
的图象上.
(1)求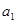 ,
, ;
;
(2)求数列 的通项公式;
的通项公式;
(3)若 ,求证数列
,求证数列 的前
的前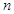 项和
项和 .
.