在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为 记
记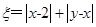 .
.
(1)求随机变量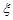 的最大值,并求事件“
的最大值,并求事件“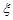 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量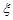 的分布列和数学期望.
的分布列和数学期望.
已知函数 ,其中
(Ⅰ)若
,求曲线
在点
处的切线方程;
(Ⅱ)若在区间
上,
恒成立,求
的取值范围.
如图,在五面体 中,四边形 是正方形, 平面 , , , , .
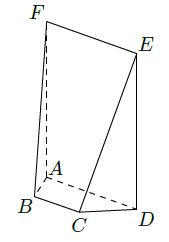
(Ⅰ)求异面直线
与
所成角的余弦值;
(Ⅱ)证明
平面
;
(Ⅲ)求二面角
的正切值。
有编号为 , ,… 的10个零件,测量其直径(单位:cm),得到下面数据:

其中直径在区间 内的零件为一等品。
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(Ⅱ)从一等品零件中,随机抽取2个.
(ⅰ)用零件的编号列出所有可能的抽取结果;
(ⅱ)求这2个零件直径相等的概率。
在
中,
.
(Ⅰ)证明
:
(Ⅱ)若
=-
,求
的值。
(本小题满分14分)
证明以下命题:
(1)对任一正整数 ,都存在正整数
,都存在正整数 ,使得
,使得 成等差数列;
成等差数列;
(2)存在无穷多个互不相似的三角形 ,其边长
,其边长 为正整数且
为正整数且 成等差数列.
成等差数列.