【2015高考上海,理19】如图,在长方体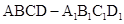 中,
中,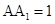 ,
,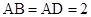 ,
,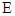 、
、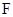 分别是
分别是 、
、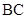 的中点.证明
的中点.证明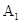 、
、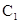 、
、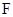 、
、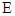 四点共面,并求直线
四点共面,并求直线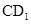 与平面
与平面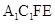 所成的角的大小.
所成的角的大小.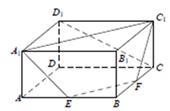
【2015高考湖南,理19】如图,已知四棱台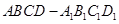 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,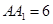 ,且
,且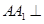 底面
底面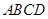 ,点
,点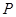 ,
,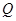 分别在棱
分别在棱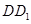 ,BC上.
,BC上.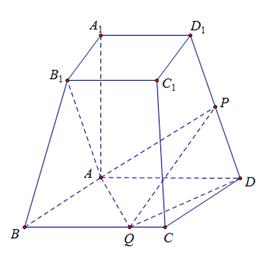
(1)若P是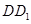 的中点,证明:
的中点,证明: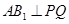 ;
;
(2)若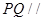 平面
平面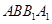 ,二面角
,二面角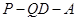 的余弦值为
的余弦值为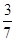 ,求四面体
,求四面体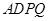 的体积.
的体积.
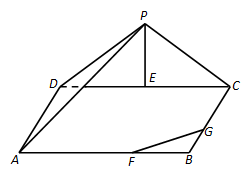
【2015高考广东,理18】如图,三角形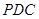 所在的平面与长方形
所在的平面与长方形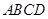 所在的平面垂直,
所在的平面垂直,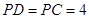 ,
,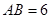 ,
,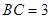 .点
.点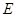 是
是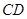 边的中点,点
边的中点,点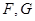 分别在线段
分别在线段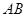 、
、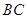 上,且
上,且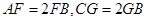 .
.
(1)证明: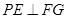 ;
;
(2)求二面角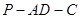 的正切值;
的正切值;
(3)求直线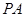 与直线
与直线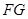 所成角的余弦值.
所成角的余弦值.
如图,在四棱锥  中,
中,  为等边三角形,平面
为等边三角形,平面  平面
平面 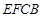 ,
,  ,
,  ,
, 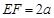 ,
,  ,
,  为
为  的中点.
的中点. 
(Ⅰ)求证:  ;
;
(Ⅱ)求二面角  的余弦值;
的余弦值;
(Ⅲ)若 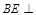 平面
平面  ,求
,求  的值.
的值.
【2015高考新课标1,理18】如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.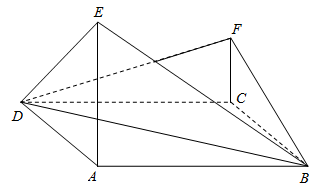
(Ⅰ)证明:平面AEC⊥平面AFC;
(Ⅱ)求直线AE与直线CF所成角的余弦值.