(本题满分10分)甲乙两地相距 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为 ,固定部分为
,固定部分为 元.
元.
(1)把全程运输成本 (元)表示为
(元)表示为 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(本小题满分13分)已知椭圆C: (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当 最小时,求点T的坐标.
最小时,求点T的坐标.
(本小题满分12分)如图,四棱锥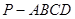 中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
(1)求三棱锥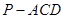 的外接球的体积;
的外接球的体积;
(2)求二面角 与二面角
与二面角 的正弦值之比.
的正弦值之比.
已知数列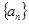 的前
的前 项和为
项和为 ,向量
,向量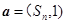 ,
, ,满足条件
,满足条件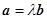 ,
, 且
且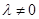 .
.
(1)求数列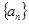 的通项公式;
的通项公式;
(2)设函数 ,数列
,数列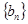 满足条件
满足条件 ,
,
①求数列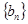 的通项公式;
的通项公式;
②设 ,求数列
,求数列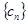 的前
的前 和
和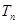 .
.
(本小题满分12分)某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数,东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.
(1)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;
(2)设 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求 的分布列和数学期望.
的分布列和数学期望.
【改编】已知函数 ,
,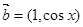
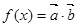
 R
R ,
, 是函数
是函数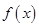 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数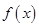 的对称轴及单调递增区间;
的对称轴及单调递增区间;
(2)若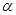
 ,且
,且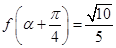 ,
, ,求
,求 的值.
的值.