如图所示的电路中,电源电动势为10V,电源内阻r=1Ω,R1= 3Ω.R 2= 6Ω.
电容C=30μF. 求:
(1)闭合开关S,稳定后通过电阻R1的电流;
(2)开关S断开后,通过R1的电荷量.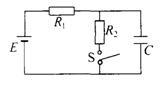
如图甲,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中。一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态。一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g。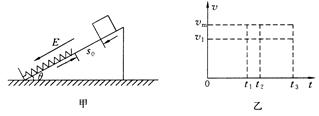
(1)求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1
(2)若滑块在沿斜面向下运动的整个过程中最大速度大小为vm,求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W;
(3)从滑块静止释放瞬间开始计时,请在乙图中画出滑块在沿斜面向下运动的整个过程中速度与时间关系v-t图象。图中横坐标轴上的t1、t2及t3分别表示滑块第一次与弹簧上端接触、第一次速度达到最大值及第一次速度减为零的时刻,纵坐标轴上的v1为滑块在t1时刻的速度大小,vm是题中所指的物理量。(本小题不要求写出计算过程)
25.如图所示,空间有场强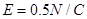 的竖直向下的匀强电场,长
的竖直向下的匀强电场,长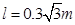 的不可伸长的轻绳一端固定于O点,另一端系一质量
的不可伸长的轻绳一端固定于O点,另一端系一质量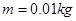 的不带电小球
的不带电小球 ,拉起小球至绳水平后,无初速释放。另一电荷量
,拉起小球至绳水平后,无初速释放。另一电荷量 、质量与
、质量与 相同的小球
相同的小球 ,以速度
,以速度 水平抛出,经时间
水平抛出,经时间 与小球
与小球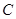 与
与 点下方一足够大的平板相遇。不计空气阻力,小球均可视为质点,取
点下方一足够大的平板相遇。不计空气阻力,小球均可视为质点,取 。
。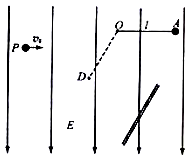
(1)求碰撞前瞬间小球 的速度。
的速度。
(2)若小球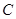 经过路
经过路 到达平板,此时速度恰好为0,求所加的恒力。
到达平板,此时速度恰好为0,求所加的恒力。
(3)若施加恒力后,保持平板垂直于纸面且与水平面的夹角不变,在 点下方面任意改变平板位置,小球
点下方面任意改变平板位置,小球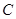 均能与平板正碰,求出所有满足条件的恒力。
均能与平板正碰,求出所有满足条件的恒力。
22. 在一次国际城市运动会中,要求运动员从高为H的平台上A点由静止出发,沿着动摩擦因数为滑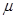 的道向下运动到B点后水平滑出,最后落在水池中。设滑道的水平距离为L,B点的高度h可由运动员自由调节(取;g=10m/s2)。求:
的道向下运动到B点后水平滑出,最后落在水池中。设滑道的水平距离为L,B点的高度h可由运动员自由调节(取;g=10m/s2)。求:
(1)运动员到达B点的速度与高度h的关系;
(2)运动员要达到最大水平运动距离,B点的高度h应调为多大?对应的最大水平距离SBH为多少?
(3若图中H=4m,L=5m,动摩擦因数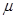 =0.2,则水平运动距离要达到7m,h值应为多少?
=0.2,则水平运动距离要达到7m,h值应为多少?
如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平面上,左端紧靠B点,上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点,运动到A时刚好与传送带速度相同,然后经A沿半圆轨道滑下,再经B滑上滑板.滑板运动到C时被牢固粘连。物块可视为质点,质量为m,滑板质量M=2m,两半圆半径均为R,板长 ,板右端到C的距离
,板右端到C的距离 在
在 范围内取值,E距A为
范围内取值,E距A为 ,物块与传送带、物块与滑板间的动摩擦因数均为
,物块与传送带、物块与滑板间的动摩擦因数均为 ,重力加速度取g.
,重力加速度取g.
(1)求物块滑到B点的速度大小;
(2)试讨论物块从滑上滑板到离开滑板右端的过程中,克服摩擦力做的功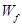 与
与 的关系,并判断物块能否滑到CD轨道的中点。
的关系,并判断物块能否滑到CD轨道的中点。
节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车。有一质量m=1000kg的混合动力轿车,在平直公路上以v1=90km/h匀速行驶,发动机的输出功率为P=50kw。当驾驶员看到前方有80km/h的限速标志时,保持发动机功率不变,立即启动利用电磁阻尼带动的发电机工作给电池充电,使轿车做减速运动,运动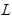 =72m后,速度变为v2=72km/h。此过程中发动机功率的
=72m后,速度变为v2=72km/h。此过程中发动机功率的 用于轿车的牵引,
用于轿车的牵引,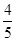 用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求
用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求
(1)轿车以90km/h在平直公路上匀速行驶时,所受阻力F阻的大小;
(2)轿车从90km/h减速到72km/h过程中,获得的电能E电;
(3)轿车仅用其在上述减速过程中获得的电能E电维持72km/h匀速运动的距离 。
。