如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一根长为L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上.将一套在杆上的带正电的小球从a端由静止释放后,小球先做加速运动,后做匀速运动到达b端。已知小球与绝缘杆间的动摩擦因数μ=0.3,小球重力忽略不计,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是L/3,求带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值。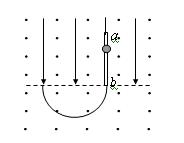
宇航员在太空中沿直线从A点运动到B点,他的运动图像如图所示,图中v是宇航员的速度,x是他的坐标。求: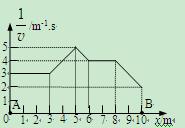
(1)宇航员从A点运动到B点所需时间。
(2)若宇航员以及推进器等装备的总质量恒为240kg,从A点到B点的过程中宇航员身上背着的推进器做功所消耗的能量为多少?
如图所示,质量为m的小球A用细绳悬挂于车顶板的O点,当小车在外力作用下沿倾角为30°的斜面向上做匀加速直线运动时,球A的悬线恰好与竖直方向成30°夹角。求:
(1)小车沿斜面向上运动的加速度多大?
(2)悬线对球A的拉力是多大?
21、如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m=1kg,电量大小为q=6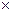 10-4C,匀强电场的场强大小为E=1
10-4C,匀强电场的场强大小为E=1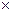 104N/C,斜轨道的倾角为α=30o,圆轨道半径R=0.8m, (小球的重力大于所受的电场力g=10m/s2) 。
104N/C,斜轨道的倾角为α=30o,圆轨道半径R=0.8m, (小球的重力大于所受的电场力g=10m/s2) 。
(1)求小球沿斜轨道下滑的加速度的大小;
(2)若使小球通过半径为R的圆轨道顶端的B点时不落下来,求A点距水平地面的高度h至少应为多大?
(3)若小球从斜轨道h =" 5R" 处由静止释放,假设能够通过B点,求在此过程中小球机械能的改变量。
、如图所示,一个带电量为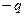 的油滴,从O点以速度
的油滴,从O点以速度 射入匀强电场中,
射入匀强电场中, 的方向与电场方向成
的方向与电场方向成 角.已知油滴的质量为
角.已知油滴的质量为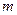 ,测得油滴到达运动轨迹的最高点时,它的速度大小又为
,测得油滴到达运动轨迹的最高点时,它的速度大小又为 .求:
.求:
(1)最高点的位置可能在O点上方的哪一侧?
(2)最高点处(设为N)与O点的电势差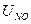 .
.
(3)电场强度 .
.
、两物块A、B用轻弹簧相连,质量均为2 kg,初始时弹簧处于原长,A、B两物块都以v=6 m/s的速度在光滑的水平地面上运动,质量4 kg的物块C静止在前方,如图所示。B与C碰撞后二者会粘在一起运动。求在以后的运动中:
(1)当弹簧的弹性势能最大时,物块A的速度为多大?
(2)系统中弹性势能的最大值是多少?