如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设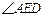 的度数为x,∠
的度数为x,∠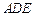 的度数为
的度数为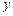 ,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.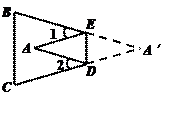
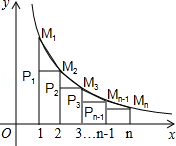
已知反比例函数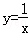 的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则
的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1,M2,M3…,Mn,则 = .
= .
已知双曲线y= 与直线y=
与直线y= 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y= 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线y= 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(﹣8,0),求A、B两点坐标及k的值;
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式;
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p﹣q的值.
如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点T(m,n)表示火炬位置,火炬从离北京路10米处的M点开始传递,到离北京路1000米的N点时传递活动结束.迎圣火临时指挥部设在坐标原点O(北京路与奥运路的十字路口),OATB为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000平方米(路线宽度均不计).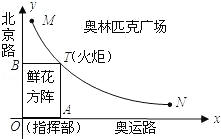
(1)求图中反比例函数的关系式(不需写出自变量的取值范围);
(2)当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示);
(3)设t=m﹣n,用含t的代数式表示火炬到指挥部的距离;当火炬离指挥部最近时,确定此时火炬的位置(用坐标表示).
如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数y= (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An﹣1An都在x轴上
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An﹣1An都在x轴上
(1)求P1的坐标;
(2)求y1+y2+y3+…y10的值.
如图,将一块直角三角形纸板的直角顶点放在C(1, )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+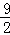 与双曲线y=
与双曲线y=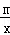 (m>0)的交点.
(m>0)的交点.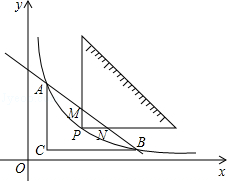
(1)求m和k的值;
(2)设双曲线y=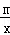 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.