如图所示，光滑水平面上有一质量M＝4.0kg的平板车，车的上表面右侧是一段水平轨道，水平轨道左侧连一半径R＝0.25m的1/4圆弧轨道，圆弧轨道与水平轨道在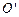
点相切．车右端C点固定一个处于自然状态的弹簧，弹簧左端恰与水平轨道上B点相齐。一质量m＝1.0kg的小物块从圆弧形轨道顶端由静止释放，小车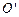B部分与小物块间摩擦系数为μ＝0.2，其余各部分摩擦不计。已知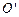B的长度L＝1m， g取10m/s2．求：
(1) 小物块经过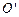点时的速度大小；
(2) 弹簧的最大弹性势能；
(3) 小物块最终离小车B点的距离。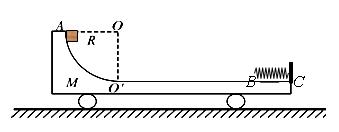
如图所示，ABCD为竖立放在场强为E＝104 V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的部分是半径为R的半圆环，轨道的水平部分与半圆环相切，A为水平轨道上的一点，而且＝R＝0.2 m．把一质量m＝0.1 kg、带电量q＝10－4 C的小球，放在水平轨道的A点由静止开始释放后，在轨道的内侧运动．(g取10 m/s2)求：
它到达C点时的速度是多大？
它到B达点时对轨道压力是多大？
若让小球安全通过D点，还从A点释放小球场强应该变为多大？
如图所示，在真空中半径r＝3.0×10－2 m的圆形区域内，有磁感应强度B＝0.2 T，方向如图的匀强磁场，一批带正电的粒子以初速度v0＝1.0×106 m/s，从磁场边界上直径ab的一端a沿着各个方向射入磁场，且初速度方向与磁场方向都垂直，该粒子的比荷为q/m＝1.0×108 C/kg，不计粒子重力．求：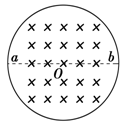
粒子的轨迹半径；
粒子在磁场中运动的最长时间
质量为m、长度为L的导体棒MN静止于水平导轨上,通过MN的电流为I,匀强磁场的磁感应强度为B,方向与导轨平面成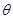
角斜向下,如图所示,求棒MN所受的支持力大小和摩擦力大小.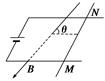
如图所示，右端带滑轮的长木板放在水平桌面上，滑块A质量为M=2kg，连接滑块A和物体B的细线质量不计，与滑轮之间的摩擦不计，滑轮与A之间的细线沿水平方向，当B的质量为1kg时，A恰好不滑动（已知最大静摩擦力与滑动摩擦力相等），g取10m/s2，求当B的质量为1.75kg时：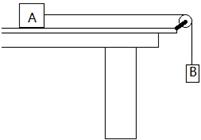
A的加速度是多大？
细线对滑轮的作用力
质量为30 kg的小孩坐在10 kg的雪橇上，大人用与水平方向成37°斜向上的大小为100 N的拉力拉雪橇，使雪橇沿水平地面向右以2m/s的速度匀速运动（sin37°=0.6,cos37°=0.8,g取10 N/kg），求：
雪橇与水平地面的动摩擦因数的大小.
突然将拉力撤去后小孩还能滑行多远？