设数列 的前n项和为
的前n项和为 ,对任意的正整数n,都有
,对任意的正整数n,都有 成立,记
成立,记 (
(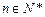 ),
),
(1)求数列 的通项公式;
的通项公式;
(2)记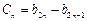 (
(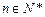 ),设数列
),设数列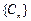 的前n和为
的前n和为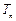 ,求证:对任意正整数n,都有
,求证:对任意正整数n,都有 .
.
(8分)已知 的顶点
的顶点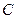
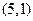 ,
,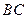 边上的中线
边上的中线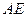 所在直线的方程为
所在直线的方程为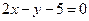 ,
,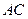 边上的高
边上的高 所在的方程为
所在的方程为 .求:
.求:
(1)顶点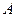 的坐标;
的坐标;
(2)直线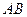 的方程.
的方程.
已知等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,公比q=2,且a2b2=20,a3b3=56,
(1)求an与bn
(2)求数列{anbn}的前n项和Tn
(3)记Cn= ,若C1+C2+C3+…+Cn≥m2﹣
,若C1+C2+C3+…+Cn≥m2﹣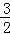 对任意正整数n恒成立,求实数m 的取值范围.
对任意正整数n恒成立,求实数m 的取值范围.
(本 题满分13分)
题满分13分)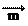 在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA=
在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA= ,向量 =
,向量 = ,
,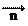
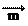
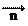 =
= ,且⊥
,且⊥
(1)求角C的值;
(2)求sinB的值;
(3)若c=5,求△ABC的面积。
某污水处理厂预计2010年底投入200万元,购入一套污水处理设备。该设备每年的运转费用是0.5 万元,此外每年都要花费一定的维护费,第一年的维护费为2万元, 由于设备老化,以后每年的维护费都比上一年增加1万元。
由于设备老化,以后每年的维护费都比上一年增加1万元。
(1)求该污水处理厂使用该设备n年 的年平均费用y(万元);
的年平均费用y(万元);
(2)为使该污水处理厂的年平均费用最低,该污水处理厂几年后需要重新更换新的污水处理设备?
已知全集为R,A={x|log2(3-x)≤2},B={x|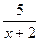 ≥1},求CR(A∩B)
≥1},求CR(A∩B)