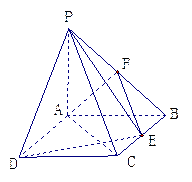
如图,四棱锥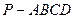 中,底面
中,底面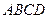 是矩形,
是矩形,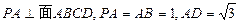 ,点
,点 是
是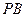 的中点,点
的中点,点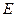 在边
在边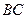 上移动。
上移动。
1)点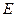 为
为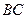 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由。
的位置关系,并说明理由。
2)证明:无论点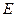 在边
在边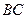 的何处,都有
的何处,都有
3)当 等于何值时,
等于何值时,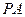 与平面
与平面 所成角的大小为
所成角的大小为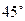 .
.
已知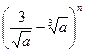 的展开式的各项系数之和等于
的展开式的各项系数之和等于 展开式中的常数项,求
展开式中的常数项,求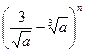 展开式中含
展开式中含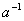 的项的二项式系数.
的项的二项式系数.
从1到9的九个数字中取三个偶数四个奇数,试问:
①能组成多少个没有重复数字的七位数?
②上述七位数中三个偶数排在一起的有几个?
③在①中的七位数中,偶数排在一起、奇数也排在一起的有几个?
④在①中任意两偶然都不相邻的七位数有几个?
若某一等差数列的首项为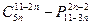 ,公差为
,公差为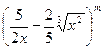 展开式中的常数项,其中m是
展开式中的常数项,其中m是 除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
求证: 能被25整除。
能被25整除。
把1、2、3、4、5这五个数字组成无重复数字的五位数,并把它们按由小到大的顺序排列成一个数列.
(1)43251是这个数列的第几项?
(2)这个数列的第96项是多少?
(3)求这个数列的各项和.