下列计算正确的是()
A.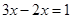 |
B.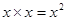 |
C.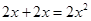 |
D.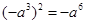 |
我市深入实施环境污染整治,某经济开发区的40家化工企业中已关停、整改32家,每年排放的污水减少了167000吨.将167000用科学记数法表示为 ()
A. |
B.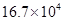 |
C.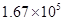 |
D. |
化简: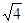 =( )
=( )
| A.2 | B.-2 | C.4 | D.-4 |
如图是某学校七年级学生跳绳成绩的条形统计图(共三等),则下面回答正确的是()
| A.C等人最少,只有40人 |
| B.该学校七年级共有120人 |
| C.A等人占总人数的30% |
D.B等人最多,占总人数的 |
某种出租车收费标准是:起步价6元(即行驶距离不超过3千米需付6元车费),超过3千米以后,每增加1千米加收1.5元(不足1千米按1千米计),某人乘这种出租车从甲地到乙地支付车费18元,设此人从甲地到乙地经过的路程为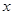 千米,则
千米,则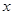 的最大值是().
的最大值是().
| A.7 | B.9 | C.10 | D.11 |