（本小题满分9分）甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．
依据统计数据绘制了如下尚不完整的统计图表．
| 分 数 |
7 分 |
8 分 |
9 分 |
10 分 |
| 人 数 |
11 |
0 |
|
8 |
（1）在图12-1中，“7分”所在扇形的圆心角等于 °．
（2）请你将图12-2的统计图补充完整．
（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好．
（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？
在Rt△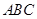
中，
，
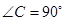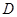为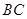
上一点，AC=5，AB=13，BD =8，
求线段AD的长度。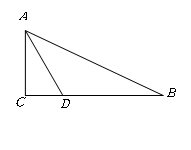
已知一个正数的平方根是a-3与2a-9，求这个正数的值。
以坐标原点为圆心，1为半径的圆分别交x，y轴的正半轴于点A，B.
（1）如图一，动点P从点A处出发，沿x轴向右匀速运动，与此同时，动点Q从点B处出发，沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢，经过1秒后点P运动到点(2,0)，此时PQ恰好是
的切线，连接OQ.求
的大小；
（2）若点Q按照（1）中的方向和速度继续运动，点P停留在点(2,0)处不动，求点Q再经过5秒后直线PQ被截得的弦长.
不透明的口袋里装有红、黄、蓝三种颜色的小球（其它一样），其中红球2个，蓝球1个，现在从中任意摸出一个红球的概率为
.
⑴.求袋中黄球的个数；
⑵.第一次摸出一个球（不放回）.第二次再摸出一个球，请用树形图或列表法求两次摸出的都是红球的概率。
如图：AB是⊙O的直径，以OA为直径的⊙O1与⊙O的弦AC相交于D，DE⊥OC，垂足为E。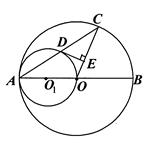
（1）求证：AD＝DC
（2）求证：DE是的切线
（3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论。