（本小题满分10分）
观察思考
某种在同一平面进行传动的机械装置如图14-1，图14-2是它的示意图．其工作原理是：滑块Q在平直滑道l上可以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研究其中所蕴含的数学知识，过点O作OH ⊥l于点H，并测得OH = 4分米，PQ = 3分米，OP = 2分米．
解决问题
（1）点Q与点O间的最小距离是 分米；点Q与点O间的最大距离是 分米；点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米．
（2）
如图14-3，小明同学说：“当点Q滑动到点H的位置时，PQ与⊙O是相切的．”你认为他的判断对吗？为什么？
（3）①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是 分米；
②当OP绕点O左右摆动时，所扫过的区域为扇形，求这个扇形面积最大时圆心角的度数．
(12分)如图(1)，点A、B、C在同一直线上，且△ABE, △BCD都是等边三角形，连结AD,CE.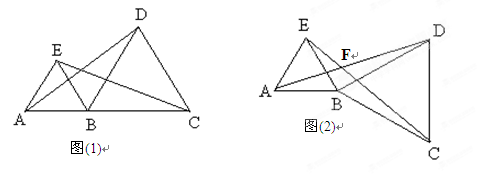
(1)△BEC可由△ABD顺时针旋转得到吗？若是，请描述这一旋转变换过程；若不是，请说明理由；
(2)若△BCD绕点B顺时针旋转，使点A,B,C不在同一直线上（如图(2)），则在旋转过程中:
①线段AD与EC的长度相等吗？请说明理由．
②锐角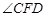
的度数是否改变？若不变，请求出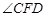的度数；若改变，请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)
(10分）如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC。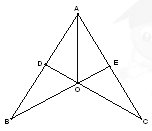
（1）求证：△ADO≌△AEO
（2）猜想OB与OC的数量关系，并说明理由.
画图题：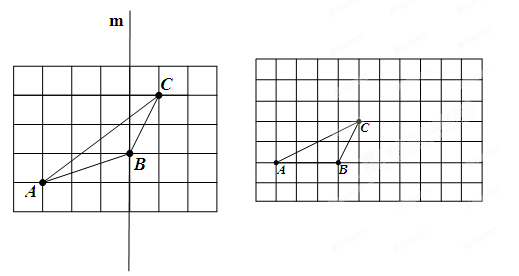
（1）如图，已知△ABC和直线m，以直线m为对称轴，画△ABC经轴对称变换后所得的像△DEF。
（2）如图：在正方形网格中有一个△ABC，按要求进行下列作图；
①画出△ABC中BC边上的高。 ②画出先将△ABC向右平移6格，再向上平移3格后的△DEF。③画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积。
市政府计划修建一处公共服务设施P，使它到AB、BC、CA三条道路的距离相等．
（1）若三条道路AB、BC、CA的位置如图所示，则图中七个区域可以修建公共设施P的区域有_____________（请将序号填在横线上）．
（2）请你选择一个区域确定公共设施P的位置（保留尺规作图痕迹，不写作法）．
如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=500，∠C=600，求∠DAE和∠BOA的度数。