（本小题满分12分）
如图16，在直角梯形ABCD中，AD∥BC，
，AD = 6，BC = 8，
，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．
设点P，Q运动的时间是t秒(t＞0)．
（1）设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式（不必写t的取值范围）．
（2）当BP = 1时，求△EPQ与梯形ABCD重叠部分的面积．
（3）随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．
已知△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D为BC边上一点．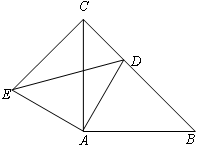
（1）求证：△ACE≌△ABD；
（2）若AC=2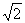
，CD=1，求ED的长．
如图，直线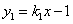
与x轴正半轴交于点A（2，0），以OA为边在x轴上方作正方形OABC，延长CB交直线
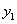于点D，再以BD为边向上作正方形BDEF．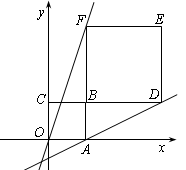
（1）求点F的坐标；
（2）设直线OF的解析式为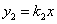
，若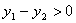
，求x的取值范围．
自古以来，钓鱼岛及其附属岛屿都是我国固有领土。如图，为了开发利用海洋资源，我勘测飞机测量钓鱼岛附属岛屿之一的北小岛（又称为鸟岛）两侧端点A、B的距离，飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了800米，在点D测得端点B的俯角为45°，求北小岛两侧端点A、B的距离.
（结果精确到0.1米，参考数据
）
如图，在菱形ABCD中，对角线AC、BD相交于点O．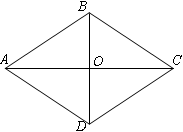
（1）平移△AOB，使得点A移动到点D，画出平移后的三角形（不写画法，保留画图痕迹）；
（2）在第（1）题画好的图形中，除了菱形ABCD外，还有哪种特殊的平行四边形？请给予证明．
解方程：（1）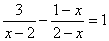
；（2）