已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.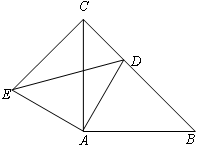
(1)求证:△ACE≌△ABD;
(2)若AC=2 ,CD=1,求ED的长.
,CD=1,求ED的长.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,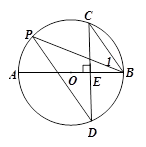
(1)求证:CB//PD;
(2)若AB=5,sin∠P=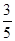 ,求BC的长.
,求BC的长.
如图:在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,AB=10,AC=6,
求D到AB的距离.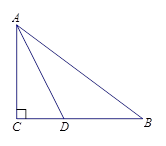
如图,一次函数y1=x+1的图象与反比例函数y2=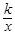 (k为常数,且k≠0)的图象都经过点A(m,2).
(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1与y2的大小.
一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,请用树状图或列表的方法列出所有可能的结果,求出两次摸出的球颜色相同的概率.
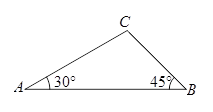
如图,在△ABC中,∠A=30°,∠B=45°,AC=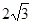 ,求AB的长.
,求AB的长.