“10米折返跑”的成绩反应了人体的灵敏素质。如图所示,测定时,在平直跑道上,受试者以站立式起跑姿势站在起点终点线前,当听到“跑”的口令后,全力跑向正前方10米处的折返线,测试员同时开始计时。受试者到达折返线时,用手触摸折返线处的物体,再转身跑向起点终点线,当胸部到达起点终点线的垂直面时,测试员停表,所用时间即为“10米折返跑”的成绩。设受试者起跑时的加速度为4m/s2,运动过程中的最大速度为4m/s,快到达折返线处时需减速到零,减速的加速度为8m/s2,返回时达到最大速度后不需减速,保持最大速度冲线。求(1)从起跑达到最大速度的时间是多少?(2)减速的距离是多少?(3)该受试者“10米折返跑”的成绩是多少?(加速、减速均视为匀变速)
如图所示,一个电容为C,极板间距为d的平行板电容器的两个极板竖直放置,在两板之间有一个质量为m的带电小球,小球用绝缘细线连接悬挂于O点。现给电容器缓慢充电,使两极板所带电量分别为+Q和-Q,此时悬线与竖直方向的夹角为30º。小球所带电量是多少?
如图所示,在长为2L、宽为L的区域内有正好一半空间有场强为E、方向平行于短边的匀强电场,有一个质量为m,电量为e的电子,以平行于长边的速度v0从区域的左上角A点射入该区域,不计电子所受重力,要使这个电子能从区域的右下角的B点射出,求:
(1)无电场区域位于区域左侧一半内时,如图甲所示,电子的初速度应满足什么条件?
(2)无电场区域的左边界离区域左边的距离为x时,如图乙所示,电子的初速度又应满足什么条件。
在图示的电路中,若R1=4Ω,R3=6Ω,电池内阻r=0.6Ω,则电源总功率为40W,输出功率为37.6W,求电源电动势和电阻R2。
如图所示,在竖直平面内,AB为水平放置的绝缘粗糙轨道,CD为竖直放置的足够长绝缘粗糙轨道,AB与CD通过四分之一绝缘光滑圆弧形轨道平滑连接,圆弧的圆心为O,半径R=0.50 m,轨道所在空间存在水平向右的匀强电场,场强的大小E=1.0×104 N/C,现有质量m=0.20 kg,电荷量q=8.0×10-4 C的带电体(可视为质点),从A点由静止开始运动,已知sAB=1.0 m,带电体与轨道AB、CD间的动摩擦因数均为0.5.假定带电体与轨道之间的最大静摩擦力和滑动摩擦力相等.求:(g=10 m/s2)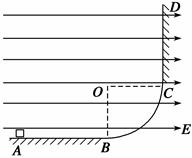
(1)带电体运动到圆弧形轨道C点时的速度;
(2)带电体最终停在何处.
如图所示电路,电源电动势E=6V,内阻r=1Ω.外电路中电阻R1=2Ω,R2=3Ω,R3=7.5Ω.电容器的电容C=4μF.求:电键S断开后,电路稳定时电容器的电量?