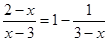（本小题满分10分）
问题再现
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.
我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如图，用正方形镶嵌平面，可以发现在一个顶点O周围围绕着4个正方形的内角.
试想：如果用正六边形镶嵌平面，在一个顶点周围应该围绕 个正六边形内角．
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：
，整理得：
，
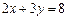我们可以找到惟一一组适合方程的正整数解为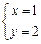
．
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．
问题拓广
请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．
一个不透明的袋子中装有4个质地、大小均相同的小球，这些小球上分别标有数字3、4、5、x．甲、乙两人每次从袋中各随机摸出1球，并计算摸出这2个小球上数字之和，记录后都将放回袋中搅匀，进行重复实验．实验数据如下表：
| 摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
| “和为8”出现频数 |
2 |
10 |
13 |
24 |
30 |
37 |
58 |
82 |
110 |
150 |
| “和为8”出现频率 |
0.20 |
0.50 |
0.43 |
0.40 |
0.33 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
解答下列问题：
(1)如果实验继续进行下去，根据上表数据，出现“和为8”频率将稳定在它概率附近．估计
出现“和为8”概率是________．
0.33
(2)如果摸出的这两个小球上数字之和为9概率是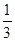
，那么x值可以取7吗？请用列表法或画树状图法说明理由；如果x值不可以取7，请写出一个符合要求x值．
某校初三所有学生参加2012年初中毕业英语口语、听力自动化考试，现从中随机抽取了部分学生的考试成绩，进行统计后分为A、B、C、D四个等级，并将统计结果绘制成如下的统计图. 请你结合图中所提供的信息，解答下列问题：(说明：A级:25分～30分；B级:20分～24分；C级:15分～19分；D级:15分以下)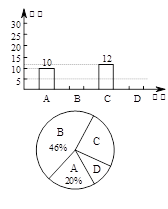
(1)请把条形统计图补充完整；
(2)扇形统计图中D级所占的百分比是_______；
(3)扇形统计图中A级所在的扇形的圆心角度数是________；
(4)若该校初三共有850名学生，试估计该年级A级和B级的学生共约为多少人
如图：E、F分别是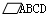 
中AD、BC边上的点，AE=CF，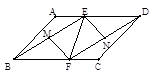
(1)求证：四边形BEDF是平行四边形；
(2)若M、N分别是BE、DF的中点，连结MF、EN、EF，当EF与BC具有怎样的位置关系时，四边形EMFN是菱形，并证明你的结论。
化简：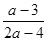
÷(
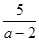-a-2)，并代入一个你喜欢的
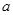值求值.
(1)计算：|－4|－(
－1)0+2cos45°－(－
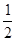)－2+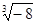
(2)解方程：