矩形OABC在平 面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-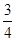 x与BC边相交于D点.
x与BC边相交于D点.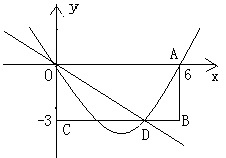
(1)若抛物线y=ax-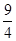 x经过点A,试确定此抛物线的解析式;
x经过点A,试确定此抛物线的解析式;
(2)在(1)中的抛物线的对称轴上取一点E,求出EA+ED的最小值;
(3)设(1)中的抛物线的对称轴与直线OD交于点M,点P为对称轴上一动点,以P、O、M为顶点的三角形与△OCD相似,求符合条件的点P的坐标.
如图,已知以Rt△ABC的直角边AB为直径做圆O,与斜边AC交于点D,E为BC边的中点,连接DE.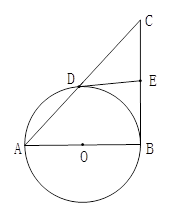
(1)求证:DE是⊙O的切线;
(2)连接OE、AE,当∠CAB为何值时,四边形AODE是平行四边形,并说明理由;
(3)在(2)的条件下,求sin∠CAE的值.
为加强对学生的爱国主义教育,某学校团组织决定在“五·四”青年节到来之际,计划租用6辆客车送一批团员师生去烈士塔参加新团员入团宣誓仪式.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车x辆,租车的总费用为y元.
| 甲种客车 |
乙种客车 |
|
| 载客量(人/辆) |
45 |
30 |
| 租金(元/辆) |
280 |
200 |
(1)求出y(元)与x(辆)之间的函数关系式,指出自变量的取值范围;
(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?
如图,反比例函数y= (k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(k>0)与矩形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S、S .
(1)①点B的坐标为;②SS(填“>”、“<”、“=”);
(2)当点D为线段AB的中点时,求k的值及点E的坐标;
(3)当S+S=2时,试判断△ODE的形状,并求△ODE的面积.
如图,△ABC是边长为5的等边三角形,将△ABC绕点C顺时针旋转120°,得到△EDC,连接BD,交AC于F.
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.