如图,△ABC是边长为5的等边三角形,将△ABC绕点C顺时针旋转120°,得到△EDC,连接BD,交AC于F.
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=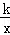 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).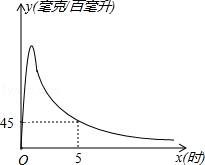
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
甲、乙、丙三位歌手进入“我是歌手”的冠、亚、季军的决赛,他们通过抽签来决定演唱顺序.
(1)求甲第一位出场的概率;
(2)求甲比乙先出场的概率.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.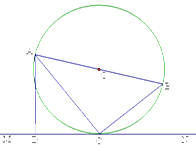
(1)猜想直线MN与⊙O的位置关系,并说明理由,
(2)若CD=6,cos∠ACD=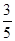 ,求⊙O的半径.
,求⊙O的半径.
如图,一台起重机,他的机身高AC为21m,吊杆AB长为40m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m).
(参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,≈1.73)
如图,在平面直角坐标系中,一次函数 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数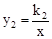 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2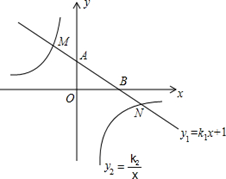
(1)求一次函数和反比例函数的解析式;
(2)直接写出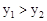 时x的取值范围.
时x的取值范围.