已知点 ,直线
,直线 :
: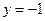 ,
,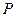 为平面上的动点,过点
为平面上的动点,过点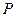 作直线
作直线 的垂线,垂足为
的垂线,垂足为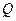 ,且
,且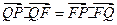 .
.
(1)求动点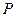 的轨迹
的轨迹 的方程;
的方程;
(2)已知圆 过定点
过定点 ,圆心
,圆心 在轨迹
在轨迹 上运动,且圆
上运动,且圆 与
与 轴交于
轴交于 、
、 两点,设
两点,设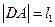 ,
, ,求
,求 的最大值.
的最大值.
已知过抛物线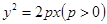 的焦点,斜率为
的焦点,斜率为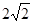 的直线交抛物线于
的直线交抛物线于
 (
( )两点,且
)两点,且 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若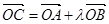 ,求
,求 的值.
的值.
已知椭圆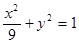 ,过左焦点F1倾斜角为
,过左焦点F1倾斜角为 的直线交椭圆于
的直线交椭圆于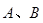 两点。求:弦AB的长。
两点。求:弦AB的长。
已知命题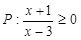 ,命题
,命题 ,若
,若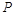 是真命题,
是真命题,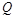 是假命题,求实数
是假命题,求实数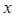 的取值范围。
的取值范围。
已知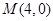 ,
,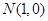 ,若动点
,若动点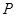 满足
满足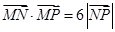 ,
,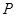 点的轨迹为曲线
点的轨迹为曲线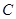 .
.
(Ⅰ)求曲线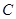 的方程;
的方程;
(Ⅱ)试确定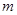 的取值范围,使得对于直线
的取值范围,使得对于直线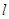 :
: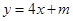 ,曲线
,曲线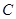 上总有不同的两点关于直线
上总有不同的两点关于直线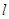 对称.
对称.
已知 是边长为
是边长为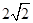 的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
(Ⅰ)求∠EOF的大小;
(Ⅱ)求二面角E-OF-A的余弦值;
(Ⅲ)求点D到面EOF的距离.