定义在 上的函数
上的函数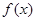 满足:对
满足:对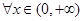 ,都有
,都有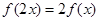 ;当
;当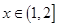 时,
时,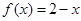 ,给出如下结论:其中所有正确结论的序号是: .
,给出如下结论:其中所有正确结论的序号是: .
①对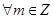 ,有
,有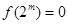 ;
;
②函数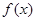 的值域为
的值域为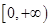 ;
;
③存在 ,使得
,使得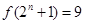 ;
;
④函数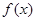 在区间
在区间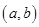 单调递减的充分条件是“存在
单调递减的充分条件是“存在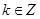 ,使得
,使得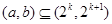 ”.
”.
(本小题满分14分)已知函数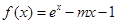 .
.
(1)当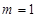 时,试判断函数
时,试判断函数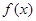 的单调性;
的单调性;
(2)对于任意的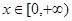 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分14分)在平面直角坐标系中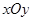 ,已知椭圆
,已知椭圆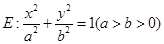 过点
过点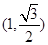 ,且椭圆
,且椭圆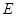 的离心率为
的离心率为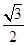 .
.
(1)求椭圆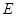 的方程;
的方程;
(2)是否存在以 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆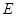 的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
(本小题满分14分)已知等差数列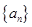 的公差
的公差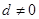 ,它的前
,它的前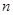 项和为
项和为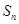 ,若
,若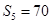 ,且
,且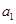 ,
,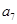 ,
,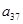 成等比数列.
成等比数列.
(1)求数列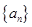 的通项公式;
的通项公式;
(2)设数列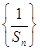 的前
的前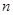 项和为
项和为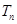 ,求证:
,求证: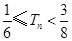 .
.
(本小题满分13分)在四棱锥 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求证: 平面
平面 ;
;
某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
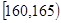 |
5 |
0.050 |
| 第2组 |
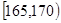 |
① |
0.350 |
| 第3组 |
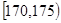 |
30 |
② |
| 第4组 |
 |
20 |
0.200 |
| 第5组 |
 |
10 |
0.100 |
| 合计 |
100 |
1.000 |
(1)请先求出频率分布表中①、②位置相应的数据;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?