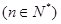如图,四棱锥P-ABCD的底面ABCD为矩形,且PA="AD=1,AB=2," 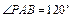 ,
,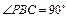 .
.
(1)求证:平面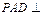 平面
平面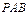 ;
;
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.
设向量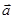 =(1,cos2θ),
=(1,cos2θ),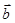 =(2,1),
=(2,1),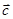 =(4sinθ,1),
=(4sinθ,1),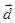 =(
=( sinθ,1),其中θ∈(0,
sinθ,1),其中θ∈(0,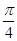 ).
).
(1)求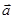 ·
·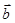 -
-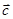 ·
·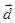 的取值范围;
的取值范围;
(2)若函数f(x)=|x-1|,比较f(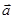 ·
·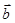 )与f(
)与f(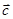 ·
·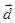 )的大小.
)的大小.
选修4—5:不等式选讲
设正有理数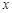 是
是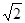 的一个近似值,令
的一个近似值,令 .
.
(Ⅰ)若 ,求证:
,求证: ;
;
(Ⅱ)比较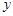 与
与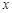 哪一个更接近于
哪一个更接近于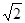 ?
?
选修4-4:坐标系与参数方程选讲.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为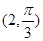 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点 ,求|MA|·|MB|。
,求|MA|·|MB|。
选修4-1:几何证明选讲.如图, 是⊙
是⊙ 的直径,
的直径,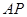 是⊙
是⊙ 的切线,
的切线,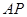 与
与 的延长线交于点
的延长线交于点 ,
, 为切点.若
为切点.若 ,
, ,
, 的平分线
的平分线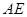 与
与 和⊙
和⊙ 分别交于点
分别交于点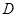 、
、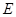 ,求
,求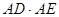 的值。
的值。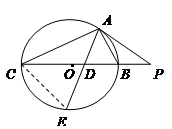
设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式: