已知椭圆E: 过点D(1,
过点D(1, ),且右焦点为F(1,0),右顶点为A.过点F的弦为BC.直线BA,直线CA分别交直线l:x=m,(m>2)于P、Q两点.
),且右焦点为F(1,0),右顶点为A.过点F的弦为BC.直线BA,直线CA分别交直线l:x=m,(m>2)于P、Q两点.

(1)求椭圆方程;
(2)若FP⊥FQ,求m的值.
(本小题满分12分)已知点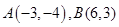 到直线
到直线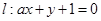 的距离相等,求
的距离相等,求 得值.
得值.
(本小题满分12分)在2015年全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲、乙两人的成绩;并根据茎叶图估计他们的中位数;
(2)已知甲、乙两人成绩的方差分别为 与
与 ,分别计算两个样本的平均数
,分别计算两个样本的平均数 和标准差
和标准差 ,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较好,哪位运动员的成绩比较稳定.
(本小题满分12分)已知一条光线从点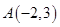 射出,经过
射出,经过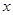 轴反射后,反射光线与圆
轴反射后,反射光线与圆 相切,求反射光线所在直线的方程.
相切,求反射光线所在直线的方程.
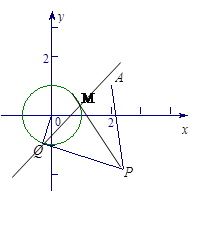
(本小题满分12分)已知圆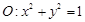 和定点
和定点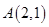 ,由圆
,由圆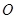 外一点
外一点 向圆
向圆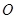 引切线
引切线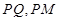 ,切点为
,切点为 ,且满足
,且满足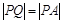 .
.
(1)求实数 间满足的等量关系;
间满足的等量关系;
(2)若以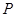 为圆心的圆
为圆心的圆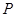 与圆
与圆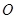 有公共点,试求圆
有公共点,试求圆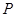 的半径最小时圆
的半径最小时圆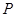 的方程;
的方程;
(3)当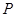 点的位置发生变化时,直线
点的位置发生变化时,直线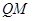 是否过定点,如果是,求出定点坐标,如果不是,说明理由.
是否过定点,如果是,求出定点坐标,如果不是,说明理由.
(本小题满分12分)在三棱锥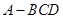 中,
中,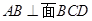 ,
, ,点
,点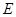 在棱
在棱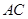 上,且
上,且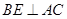 .
.
(Ⅰ)试证明: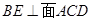 ;
;
(Ⅱ)若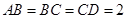 ,过直线
,过直线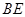 任作一个平面与直线
任作一个平面与直线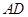 相交于点
相交于点 ,得到三棱锥
,得到三棱锥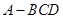 的一个截面
的一个截面 ,求
,求 面积的最小值;
面积的最小值;
(Ⅲ)若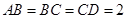 ,求二面角
,求二面角 的正弦值.
的正弦值.