已知函数 ,
, ,
,
(Ⅰ)当 时,若
时,若 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当 是整数时,存在
是整数时,存在 ,使得
,使得 是
是 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在 ,且
,且 上的函数
上的函数 ,使当
,使当 时,
时, ,当
,当 时,
时, 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
(本小题满分12分)
在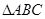 中,
中,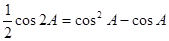 .
.
(I)求角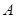 的大小;
的大小;
(II)若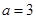 ,
,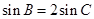 ,求
,求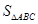 .
.
(设函数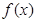 在
在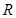 上满足
上满足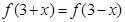 ,
,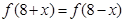 ,且
,且
在闭区间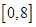 上只有
上只有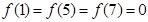 .
.
(1)求证函数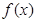 是周期函数;
是周期函数;
(2)求函数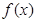 在闭区间
在闭区间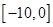 上的所有零点;
上的所有零点;
(3)求函数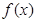 在闭区间
在闭区间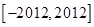 上的零点个数及所有零点的和.
上的零点个数及所有零点的和.
10分)某太阳能热水器厂2007年的年生产量为670台,该年比上一年的年产量的
增长率为34%. 从2008年开始,以后的四年中,年生产量的增长率逐年递增2%(如,2008
年的年生产量的增长率为36%).
(1)求2008年该厂太阳能热水器的年生产量(结果精确到0.1台);
(2)求2011年该厂太阳能热水器的年生产量(结果精确到0.1台);
(3)如果2011年的太阳能热水器的实际安装量为1420台,假设以后若干年内太阳能热水
器的年生产量的增长率保持在42%,到2015年,要使年安装量不少于年生产量的95%,这四
年中太阳能热水器的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
(参考数据: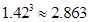 ,
,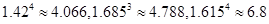 ,1.5634="5.968" ).
,1.5634="5.968" ).
(若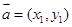 ,
,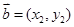 ,定义:
,定义: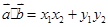
已知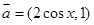 ,
,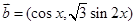 ,
,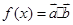 ,
,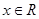
(1)若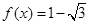 ,且
,且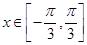 ,求
,求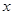 ;
;
(2)若函数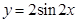 的图象向左(或右)平移
的图象向左(或右)平移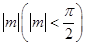 个单位,再向上(或
个单位,再向上(或
(3)下)平移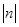 个单位后得到函数
个单位后得到函数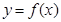 的图象,求实数
的图象,求实数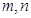 的值.
的值.
已知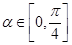 ,
,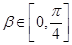 且
且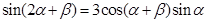 ,
,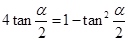 ,求
,求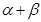 的值.
的值.