(本小题满分13分)已知:函数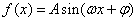 (其中
(其中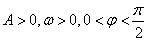 )的
)的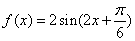 图象与
图象与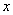 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为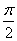 ,且图象上一个最低点为
,且图象上一个最低点为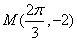 。
。
(1)求: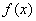 的解析式; (2)当
的解析式; (2)当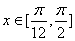 ,求:函数
,求:函数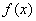 的值域。
的值域。
(本题共13分,第Ⅰ问6分,第Ⅱ问7分)
在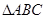 中,角
中,角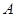 、
、 、
、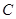 所对的边分别为
所对的边分别为 、
、 、
、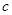 ,且
,且 .
.
(Ⅰ)求角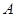 的大小;(Ⅱ)若
的大小;(Ⅱ)若 ,求
,求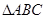 面积的最大值.
面积的最大值.
(本题共13分,第Ⅰ问6分,第Ⅱ问7分)
现有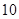 道题,其中
道题,其中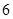 道甲类题,
道甲类题,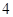 道乙类题,张同学从中任取
道乙类题,张同学从中任取 道题解答.
道题解答.
(Ⅰ)求张同学至少取到 道乙类题的概率;
道乙类题的概率;
(Ⅱ)已知所取的 道题中有2道甲类题,
道题中有2道甲类题, 道乙类题.设张同学答对甲类题的概率都是
道乙类题.设张同学答对甲类题的概率都是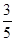 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是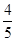 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求 的分布列和数学期望
的分布列和数学期望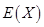 .
.
(本题共13分,第Ⅰ问6分,第Ⅱ问7分)
已知函数 .
.
(Ⅰ)求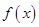 的最小正周期;
的最小正周期;
(Ⅱ)求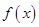 的单调递增区间,并求出
的单调递增区间,并求出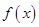 在
在 上的最大值与最小值.
上的最大值与最小值.
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)已知椭圆 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,离心率
轴上,离心率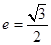 ,过椭圆
,过椭圆 右焦点且垂直于
右焦点且垂直于 轴的一条直线交椭圆于
轴的一条直线交椭圆于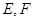 两点,
两点,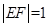 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知两点 ,设
,设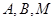 是椭圆
是椭圆 上的三点,满足
上的三点,满足 ,点
,点 为线段
为线段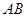 的中点,求
的中点,求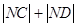 的值.
的值.
(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分)一家公司计划生产某种小型产品的月固定成本为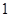 万元,每生产
万元,每生产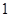 万件需要再投入
万件需要再投入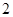 万元.设该公司一个月内生产该小型产品
万元.设该公司一个月内生产该小型产品 万件并全部销售完,每万件的销售收入为
万件并全部销售完,每万件的销售收入为 万元,且每万件国家给予补助
万元,且每万件国家给予补助 万元. (
万元. (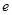 为自然对数的底数,
为自然对数的底数,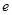 是一个常数.)
是一个常数.)
(Ⅰ)写出月利润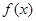 (万元)关于月产量
(万元)关于月产量 (万件)的函数解析式;
(万件)的函数解析式;
(Ⅱ)当月生产量在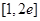 万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).