(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分)一家公司计划生产某种小型产品的月固定成本为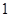 万元,每生产
万元,每生产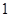 万件需要再投入
万件需要再投入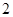 万元.设该公司一个月内生产该小型产品
万元.设该公司一个月内生产该小型产品 万件并全部销售完,每万件的销售收入为
万件并全部销售完,每万件的销售收入为 万元,且每万件国家给予补助
万元,且每万件国家给予补助 万元. (
万元. (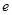 为自然对数的底数,
为自然对数的底数,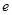 是一个常数.)
是一个常数.)
(Ⅰ)写出月利润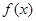 (万元)关于月产量
(万元)关于月产量 (万件)的函数解析式;
(万件)的函数解析式;
(Ⅱ)当月生产量在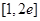 万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
设数列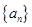 的前
的前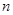 项和为
项和为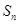 ,且
,且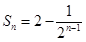 .
.
(1)求数列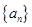 的通项公式;
的通项公式;
(2)设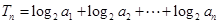 ,求证:
,求证: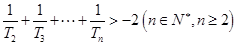 .
.
在如图的多面体中,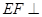 平面
平面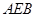 ,
,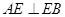 ,
,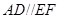 ,
,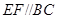 ,
,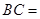
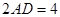 ,
,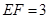 ,
, ,
,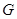 是
是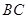 的中点.
的中点.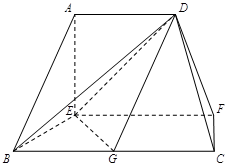
(1)求证: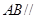 平面
平面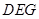 ;
;
(2)求证: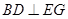 ;
;
(3)求三棱锥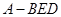 的体积.
的体积.
随着工业化的发展,环境污染愈来愈严重.某市环保部门随机抽取60名市民对本市空气质量满意度打分,把数据分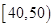 、
、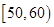 、
、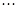 、
、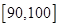 六段后得到如下频率分布表:
六段后得到如下频率分布表:
| 分组 |
频数 |
频率 |
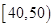 |
 |
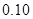 |
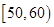 |
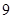 |
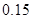 |
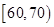 |
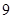 |
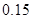 |
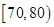 |
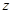 |
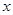 |
 |
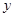 |
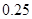 |
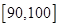 |
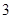 |
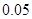 |
| 合计 |
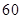 |
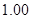 |
(1)求表中数据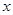 、
、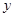 、
、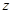 的值;
的值;
(2)用分层抽样的方法在分数 的市民中抽取容量为
的市民中抽取容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取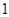 人在分数段
人在分数段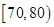 的概率.
的概率.
已知函数 ,
, .
.
(1)当 为何值时,
为何值时, 取得最大值,并求出其最大值;
取得最大值,并求出其最大值;
(2)若 ,
, ,求
,求 的值.
的值.
已知点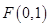 直线
直线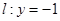 ,
,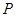 为平面上的动点,过点
为平面上的动点,过点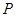 作直线
作直线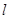 的垂线,垂足为
的垂线,垂足为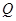 ,且
,且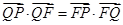 .
.
(1)求动点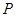 的轨迹方程;
的轨迹方程;
(2)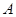 、
、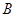 是轨迹
是轨迹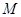 上异于坐标原点
上异于坐标原点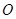 的不同两点,轨迹
的不同两点,轨迹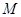 在点
在点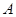 、
、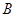 处的切线分别为
处的切线分别为 、
、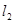 ,且
,且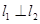 ,
, 、
、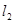 相交于点
相交于点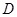 ,求点
,求点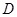 的纵坐标.
的纵坐标.