如图,正四棱锥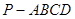 中,侧棱
中,侧棱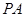 与底面
与底面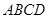 所成角的正切值为
所成角的正切值为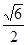 .
.
(1)求侧面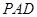 与底面
与底面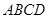 所成二面角的大小;
所成二面角的大小;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.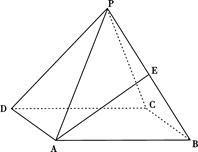
已知数列 满足
满足 ,其中
,其中 是数列
是数列 的前
的前 项和.
项和.
(1)若数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,求数列
的等比数列,求数列 的通项公式;
的通项公式;
(2)若 ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(3)在(2)的条件下,设 ,求证:数列
,求证:数列 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.
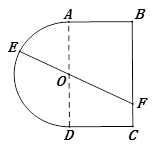
一个玩具盘由一个直径为 米的半圆
米的半圆 和一个矩形
和一个矩形 构成,
构成,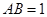 米,如图所示.小球从
米,如图所示.小球从 点出发以
点出发以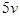 的速度沿半圆
的速度沿半圆 轨道滚到某点
轨道滚到某点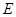 处后,经弹射器以
处后,经弹射器以 的速度沿与点
的速度沿与点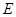 切线垂直的方向弹射到落袋区
切线垂直的方向弹射到落袋区 内,落点记为
内,落点记为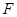 .设
.设 弧度,小球从
弧度,小球从 到
到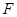 所需时间为
所需时间为 .
.
(1)试将 表示为
表示为 的函数
的函数 ,并写出定义域;
,并写出定义域;
(2)求时间 最短时
最短时 的值.
的值.
如图,在三棱锥 中,
中, ,
, ,点
,点 ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:
 .
.
在 中,角
中,角 的对边分别为
的对边分别为 ,向量
,向量 .
.
(1)若 ,求证:
,求证: ;
;
(2)若 ,
, ,求
,求 的值.
的值.
已知函数 ,设数列
,设数列 满足:
满足: ,
, .
.
(1)求证: ,都有
,都有 ;
;
(2)求证: