已知偶函数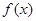 ,对任意
,对任意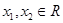 ,恒有
,恒有 。求:
。求:
(1) ,
,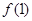 ,
,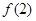 的值;
的值;
(2)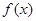 的表达式;
的表达式;
(3) 在
在 上的最值。
上的最值。
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中,M是BD的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)求证:ME∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面BDE? 若存在,确定点N的位置;若不存在,请说明理由.
已知 的顶点A(0,1),AB边上的中线CD所在直线方程为
的顶点A(0,1),AB边上的中线CD所在直线方程为 ,AC边上的高BH所在直线方程为
,AC边上的高BH所在直线方程为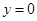 .
.
(1)求 的项点B、C的坐标;
的项点B、C的坐标;
(2)若圆M经过不同的三点A、B、P(m、0),且斜率为1的直线与圆M相切于点P
求:圆M的方程.
在三棱锥 中,
中, 是边长为
是边长为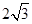 的正三角形,平面
的正三角形,平面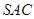 ⊥平面
⊥平面 ,
, ,
,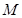 、
、 分别为
分别为 、
、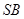 的中点.
的中点.
(1)证明: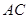 ⊥
⊥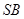 ;
;
(2)求三棱锥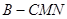 的体积.
的体积.
已知圆 交于
交于 两点.
两点.
(1)求过A、B两点的直线方程;
(2)求过 两点且圆心在直线
两点且圆心在直线 上的圆的方程.
上的圆的方程.