(本小题满分15分)
已知函数 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: 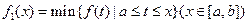 ,
,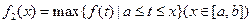
其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 在
在 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得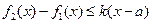 对任意的
对任意的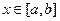 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(1)若 ,
, ,试写出
,试写出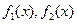 的表达式;
的表达式;
(2)已知函数 ,
,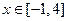 ,试判断
,试判断 是否为
是否为 上的“
上的“ 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(3)已知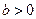 ,函数
,函数 是
是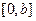 上的2阶收缩函数,求
上的2阶收缩函数,求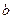 的取值范围.
的取值范围.
已知函数 (
( 为实常数).
为实常数).
(Ⅰ) 若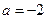 ,求证:函数
,求证:函数 在
在 上是增函数;
上是增函数;
(Ⅱ) 求函数 在
在 上的最小值及相应的
上的最小值及相应的 值;
值;
(Ⅲ) 若存在 ,使得
,使得
 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知指数函数 满足:
满足: ,定义域为
,定义域为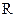 的函数
的函数 是奇函数。(Ⅰ)求
是奇函数。(Ⅰ)求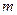 ,
, 的值;(Ⅱ)若对任意的
的值;(Ⅱ)若对任意的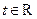 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分15分) 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
(2)证明:直线PQ与圆O相切.
(本小题满分15分)已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
(本小题满分16分)设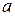 为实数,函数
为实数,函数 .(1)若
.(1)若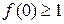 ,求
,求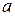 的取值范围;(2)求
的取值范围;(2)求 的最小值;(3)设函数
的最小值;(3)设函数 ,求不等式
,求不等式 的解集.
的解集.