(1)计算:(p-2010)0 +(sin60°)-1-︱tan30°-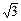 ︱+
︱+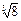 .
.
(2)先化简: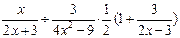 ;若结果等于
;若结果等于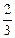 ,求出相应x的值.
,求出相应x的值.
小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后分钟时,他所在的位置与家的距离为 千米,且
千米,且 与之间的函数关系的图像如图中的折线段
与之间的函数关系的图像如图中的折线段 所示.
所示.
(1)试求折线段 所对应的函数关系式;
所对应的函数关系式;
(2)请解释图中线段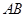 的实际意义;
的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离 (千米)与小明出发后的时间(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
(千米)与小明出发后的时间(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,它造成的雾霾天气对人体健康的危害甚至要比沙尘暴更大。环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5检测,某日随机抽取25个监测点的研究性数据,并绘制成统计表和扇形统计图如下: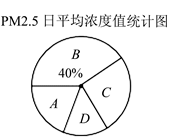
| 类别 |
组别 |
PM2.5日平均浓度值 (微克/立方米) |
频数 |
频率 |
| A |
1 |
15~30 |
2 |
0.08 |
| 2 |
30~45 |
3 |
0.12 |
|
| B |
3 |
45~60 |
a |
b |
| 4 |
60~75 |
5 |
0.20 |
|
| C |
5 |
75~90 |
6 |
c |
| D |
6 |
90~105 |
4 |
0.16 |
| 合计 |
以上分组均含最小值,不含最大值 |
25 |
1.00 |
根据图表中提供的信息解答下列问题:
(1)统计表中的 = _,b=_,c=_;
= _,b=_,c=_;
(2)在扇形统计图中,A类所对应的圆心角是_度;
(3)我国PM2.5安全值的标准采用世卫组织(WHO)设定的最宽限值:日平均浓度小于75微克/立方米.请你估计当日环保监测中心在检测100个城市中,PM2.5日平均浓度值符合安全值的城市约有多少个?
在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是_;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表法求解).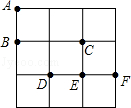
如图,在平行四边形ABCD中,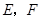 为
为 上两点,且
上两点,且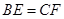 ,
,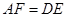 .
.
求证:(1)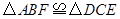 ;
;
(2)四边形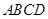 是矩形.
是矩形.