数学课上，李老师出示了这样一道题目：如图
，正方形
的边长为
，
为边
延长线上的一点，
为
的中点，的垂直平分线交边
于
，交边
的延长线于
.当
时，
与
的比值是多少？
经过思考，小明展示了一种正确的解题思路：过作直线平行于交，分别于
，
，如图
，则可得：
，因为
，所以
.可求出
和
的值，进而可求得与的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究，得出了
的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.
阅读下面的文字，解答问题．
大家知道
是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，但是由于1<<2，所以的整数部分为1，将减去其整数部分1，差就是小数部分－1，根据以上的内容，解答下面的问题：
（1）
的整数部分是_______，小数部分是______；
（2）1＋的整数部分是_______，小数部分是____；
（3）若设2＋
的整数部分是x，小数部分是y，求x－y的值
如图所示，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M、N重合，过角尺顶点C的射线OC便是∠AOB的平分线，为什么?
两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，在同一条直线上，连结DC．请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）．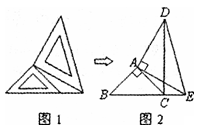
小明某天上午9时骑自行车离开家，15时回家，他有意描绘了离家的距离与时间的变化情况（如图所示）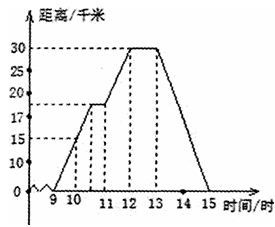
（1）10时和13时，他分别离家多远?
（2）他到达离家最远的地方是什么时间?离家多远?
（3）他由离家最远的地方返回时的平均速度是多少?
如图所示，由小正方形组成的L形图中，请你用三种方法分别在下图中再添画一个小正方形使它成为轴对称图形：