如图,在平面直角坐标系中,顶点为( ,
, )的抛物线交
)的抛物线交 轴于
轴于 点,交
点,交 轴于
轴于 ,
, 两点(点
两点(点 在点
在点 的左侧). 已知
的左侧). 已知 点坐标为(
点坐标为( ,
, ).
).
(1)求此抛物线的解析式;
(2)过点 作线段
作线段 的垂线交抛物线于点
的垂线交抛物线于点 , 如果以点
, 如果以点 为圆心的圆与直线
为圆心的圆与直线 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴 与⊙
与⊙ 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 ,
, 两点之间,问:当点
两点之间,问:当点
(本小题6分)x、y为实数,且 ,求
,求 的值
的值
(本小题4分)今年端午节,某乡镇成立一支龙舟队,共30名队员,他们的身高情况如下表:
根据表中的信息回答以下问题:
(1)龙舟队员身高的众数是______,中位数是______;
(2)这30名队员平均身高是多少cm?身高大于平均身高的队员占全队的百分之几?
(本小题7分)在生活中,我们知道大气压随着高度的增加而减小,设离海平面2km内,山高y(km)与大气压x(cmHg)关系如下表: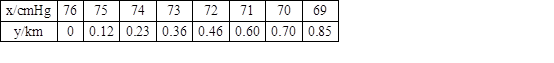
(1)在平面直角坐标系中作出各有序数对(x,y)所对应的点;
(2)这些点是否近似地在一条直线上?
(3)写出x与y之间的一个近似表达式;
(4)估计当大气压为64cmHg时山的高度.
(本小题6分)如图,已知平行四边形ABCD中,E、F分别BC、AD边上,AE=BF,AE与BF交于G,ED与CF交于H.
求证:(1)GH∥BC;
(2)GH= AD
AD
(本小题4分)如图,在四边形ABCD中,已知AB:BC:CD:DA=2:2:3:1,且∠B=90°,求∠DAB的度数.