已知F1、F2是双曲线 的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )
A.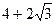 |
B.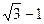 |
C.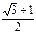 |
D.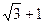 |
设函数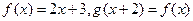 ,则
,则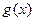 的表达式是()
的表达式是()
A.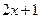 |
B.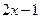 |
C.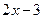 |
D.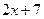 |
若直线mx—ny = 4与⊙O: x2+y2= 4没有交点,则过点P(m,n)的直线与椭圆 的交点个数是()
的交点个数是()
| A.至多为1 | B.2 | C.1 | D.0 |
如果AC<0,且BC<0,那么直线Ax+By+C=0不通过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
当a为任意实数时,直线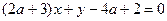 恒过定点P,则过点P的抛物线的标准方程是()
恒过定点P,则过点P的抛物线的标准方程是()
A.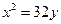 或 或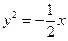 |
B. 或 或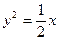 |
C.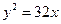 或 或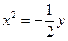  |
D.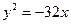 或 或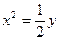 |
如图,在四棱锥P -ABCD中,侧面PAD为正三角形,底面为正方
-ABCD中,侧面PAD为正三角形,底面为正方
形,侧面PAD与底面ABCD垂直,M为底面内的一个动点,且满足MP=MC,则动点M的轨迹为 ()
| A.椭圆 | B.抛物线 |
| C.双曲线 | D.直线 |