（本小题满分12分）正在执行护航任务的某导弹护卫舰，突然收到一艘商船的求救信号，紧急前往相关海域．如图所示，到达相关海域
处后发现，在南偏西
、5海里外的洋面M处有一条海盗船，它正以每小时20海里的速度向南偏东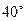
的方向逃窜．某导弹护卫舰当即施放载有突击队员的快艇进行拦截，快艇以每小时30海里的速度向南偏东
的方向全速追击．请问：快艇能否追上海盗船？如果能追上，请求出
的值；如果未能追上，请说明理由．
已知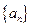
为等差数列，且
，
。
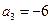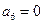（Ⅰ）求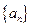的通项公式；
（Ⅱ）若等比数列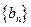
满足
，
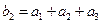，求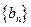的前n项和公式。
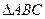的面积是30，内角
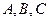所对边长分别为
，
。
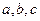(Ⅰ)求
；
(Ⅱ)若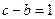
，求
的值。
为了迎接2010年在广州举办的亚运会，我市某体校计划举办一次宣传活动，届时将在运动场的一块空地ABCD（如图）上摆放花坛，已知运动场的园林处（P点）有一批鲜花，今要把这批鲜花沿道路PA或PB送到空地ABCD中去，且PA="200" m，PB="300" m，∠APB=60°.
（1）试求A、B两点间的距离；
（2）能否在空地ABCD中确定一条界线，使位于界线一侧的点，沿道路PA送花较近；而另一侧的点，沿道路PB送花较近？如果能，请说出这条界线是一条什么曲线，并求出其方程.
将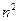
个数排成
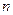行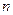列的一个数阵：
已知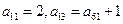
，该数列第一列的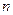个数从上到下构成以
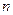为公差的等差数列，每一行的个数从左到右构成以为公比的等比数列，其中为正实数。
（1）求m;
（2）求第
行第1列的数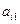
及第行第
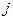列的数
（3）求这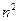个数的和。
已知直线l经过抛物线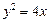
的焦点F，且与抛物线相交于A、B两点.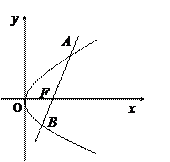
（1）若
，求点A的坐标；
（2）若直线l的倾斜角为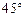
，求线段AB的长.