在平面直角坐标系xOy中，设直线y＝
x＋2m和圆x2＋y2＝n2相切，其中m，n∈N*，0＜| m－n |≤1，若函数f (x)＝mx+1－n的零点x0∈（k，k＋1），k∈Z，则k＝
已知圆M：（x＋cosq）2＋（y－sinq）2＝1，直线l：y＝kx，下面四个命题
①对任意实数k与q，直线l和圆M相切；
②对任意实数k与q，直线l和圆M有公共点；
③对任意实数q，必存在实数k，使得直线l与和圆M相切;
④对任意实数k，必存在实数q，使得直线l与和圆M相切.
其中真命题的代号是______________（写出所有真命题的代号）.
如右图，过原点O作⊙O1：x2＋y2－6x－8y＋20＝0的两条切线，设切点分别为P、Q，则线段PQ的长为________．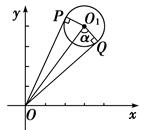
若关于x的不等式|x＋2|＋|x－1|<a的解集为
，则实数a的取值范围为___________.
若⊙O：x2＋y2＝5与⊙O1：(x－m)2＋y2＝20(m∈R)外切，则实数
___________.
已知圆C的圆必是抛物线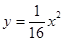
的焦点。直线4x-3y-3=0与圆C相交于A，B两点，且|AB|=8，则圆C的方程为。