14分)已知椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1),且其右焦点到直线x-y+ =0的距离为3.(I)求椭圆的方程;
=0的距离为3.(I)求椭圆的方程;
(II)是否存在斜率为k(k≠0)的直线l,使l与已知椭圆交于不同的两点M、N,
且|AN|=|AM|?若存在,求出k的取值范围;若不存在,请说明理由.
已知向量 ,
, ,函数f(x)=
,函数f(x)= ,且y=f(x)的图象过点
,且y=f(x)的图象过点 和点
和点 .
.
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
选修4—5:不等式选讲
已知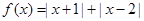 ,
,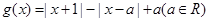 .
.
(Ⅰ)解不等式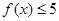 ;
;
(Ⅱ)若不等式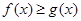 恒成立,求a的取值范围.
恒成立,求a的取值范围.
选修4—4:极坐标与参数方程
已知圆的极坐标方程为: .
.
(Ⅰ)将极坐标方程化为普通方程;并选择恰当的参数写出它的参数方程;
(Ⅱ)若点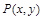 在该圆上,求
在该圆上,求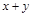 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)已知函数 ,其中e为自然对数的底数,a为常数.
,其中e为自然对数的底数,a为常数.
(1)若对函数 存在极小值,且极小值为0,求a的值;
存在极小值,且极小值为0,求a的值;
(2)若对任意 ,不等式
,不等式 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(本小题满分12分)在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且 .
.
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.