(理科)已知以原点 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为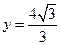 ,离心率
,离心率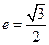 ,
,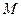 是椭圆上的动点.
是椭圆上的动点.
(1)若点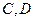 的坐标分别是
的坐标分别是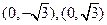 ,求
,求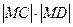 的最大值;
的最大值;
(2)如图,点 的坐标为
的坐标为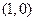 ,
,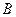 是圆
是圆 上的点,点
上的点,点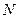 是点
是点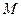 在
在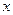 轴上的射影,点
轴上的射影,点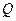 满足条件:
满足条件: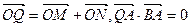 ,求线段
,求线段 的中点
的中点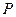 的轨迹方程.
的轨迹方程.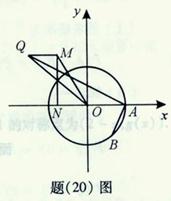
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.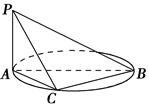
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值..
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.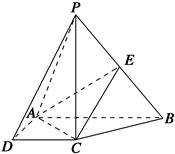
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为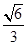 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
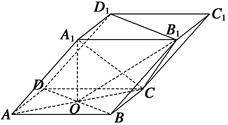
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=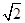 .
.
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=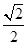 AB.
AB.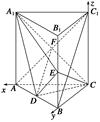
(1)证明:BC1∥平面A1CD;
(2)求二面角D-A1C-E的正弦值.
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为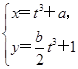 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.