(本小题满分12分)
如图,在直三棱柱 中,
中,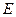 、
、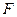 分别是
分别是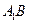 、
、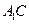 的中点,点
的中点,点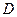 在
在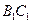 上,
上, 。
。
求证:(1)EF∥平面ABC;
(2)平面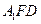
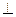 平面
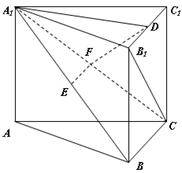
平面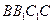 .
.
(本小题满分14分)
某网店对一应季商品过去20天的销售价格及销售量进行了监测统计发现,第 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 天的销售量为
天的销售量为 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.
(Ⅰ)写出销售额 关于第
关于第 天的函数关系式;
天的函数关系式;
(Ⅱ)求该商品第7天的利润;
(Ⅲ)该商品第几天的利润最大?并求出最大利润.
(本小题满分12分)
已知函数 .
.
(Ⅰ)若 为偶函数,求
为偶函数,求 的值;
的值;
(Ⅱ)若 在
在 上有最小值9,求
上有最小值9,求 的值.
的值.
(本小题满分12分)
如图,四棱锥 的底面
的底面 是菱形,
是菱形, ,
, 面
面 ,
, 是
是 的中点,
的中点, 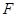 是
是 的中点.
的中点.
(Ⅰ)求证:面 ⊥面
⊥面 ;
;
(Ⅱ)求证: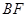 ∥面
∥面 .
.
(本小题满分12分)
已知 的三个顶点
的三个顶点 .
.
(Ⅰ)求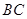 边所在直线方程;
边所在直线方程;
(Ⅱ)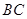 边上中线
边上中线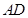 的方程为
的方程为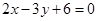 ,且
,且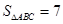 ,求
,求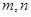 的值.
的值.
(本小题满分12分)已知函数 满足
满足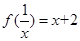 .
.
(Ⅰ)求 的解析式及其定义域;
的解析式及其定义域;
(Ⅱ)写出 的单调区间并证明.
的单调区间并证明.