(本小题满分14分)如图,在三棱锥 中,
中,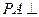 底面
底面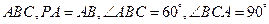 ,
,
点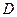 ,
, 分别在棱
分别在棱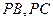 上,且
上,且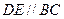


(1)求证: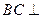 平面
平面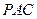 ;
;
(2)当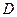 为
为 的中点时,求
的中点时,求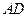 与平面
与平面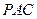 所成的角的正弦值;
所成的角的正弦值;
(3)是否存在点 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.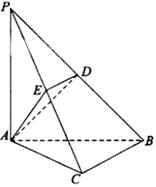
(本小题满分12分)如图,在三棱柱 中,已知
中,已知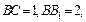
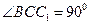 ,
, 侧面
侧面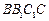

(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱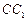 (不包含端点
(不包含端点 上确定一点
上确定一点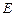 的位置,使得
的位置,使得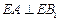 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若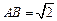 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分12分)
已知数列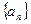 中,
中,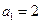 ,
,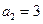 ,其前
,其前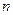 项和
项和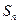 满足
满足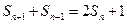 (
(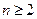 ,
,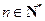
(1)求数列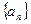 的通项公式;
的通项公式;
(2)设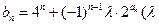 为非零整数,
为非零整数,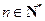 ),试确定
),试确定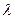 的值,使得对任意
的值,使得对任意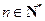 ,都有
,都有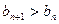 成立.
成立.
(本小题满分12分)由于当前学生课业负担较重,造成青少年视力普遍下降,现从湖口中学随机抽取16名学生,经校医用对数视力表检查得到每 个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“good sight”,求校医从这16人中随机选取3人,至多有1人是“good sight”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记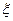 表示抽到“good sight”学生的人数,求
表示抽到“good sight”学生的人数,求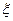 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)已知角A、B、C是 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, 。
。
(1)求角A的大小;(2)若 求
求 的长。
的长。
已知向量 ,
, ,其中
,其中 ,设
,设 ,且函数
,且函数 的最大值为
的最大值为 .。
.。
(Ⅰ)求函数 的解析式。
的解析式。
(Ⅱ)设 ,求函数
,求函数 的最大值和最小值以及对应的
的最大值和最小值以及对应的 值。
值。