在跳水馆里，水池里水的深度要恰当。水太深，会造成浪费，太浅则会使跳水运动员的在比赛中存在危险。下面我们可以用学过的物理知识，再将跳水运动进行理想化处理，就可以大体上估算出水池里水的深度至少是多少。在10m跳台跳水比赛中，运动员起跳高度取0.5m，运动员入水后将会受到浮力、水的阻力等，入水速度越大，水的阻力也会越大。在下列情况下估算水池的安全深度。
（1）运动员从最高点向下运动认为是自由落体运动，若运动员入水后受到的浮力和水的阻力总共为自身重量的3倍。求出水池的安全深度。
（2）运动员从最高点向下运动认为是自由落体运动，运动员入水后受到的水的阻力很大，如果不考虑水的阻力，只考虑浮力，计算的安全深度将有很大偏差。若运动员的身体的密度是水的密度的0.9倍，入水后在只考虑浮力和重力的情况下，计算水池的安全深度。
（3）实际上，运动员在空中的运动也受空气阻力，若空气阻力是重力的0.2倍，仍按照运动员入水后受到的浮力和水的阻力总共为自身重量的3倍。计算水池的安全深度。
右端连有光滑弧形槽的水平桌面AB长L="1.5" m，如图。使一个质量为m=0.5kg的木块在F="1.5" N的水平拉力作用下，从桌面上A端由静止开始向右运动，木块到达B端时撤去拉力F，木块与水平桌面间动摩擦因数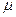
=0.2，取g= l0m/s2。求：
（1）木块沿弧形槽上升的最大高度？
（2）木块沿弧形槽滑回B端后，在木板上滑动的最大距离？
继神秘的火星之后，近几年土星也成了世界关注的焦点。经过近7年、2亿千米在太空中风尘仆仆的穿行后，美航天局和欧航天局合作研究出“卡西尼”号土星探测器抵达预定轨道，开始“拜访”土星及其卫星家族。这是人类首次针对土星及其31颗已知卫星最详尽的探测。若“卡西尼”号土星探测器进入土星飞行的孰道，在半径为R的土星上空离土星表面高h的圆形轨道上绕土星飞行，环绕n周飞行时间为t，求：
（1）“卡西尼”号土星探测器绕土星飞行的周期。
（2）土星的质量。
如图所示，固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在口点平滑连接，轨道半径R=0.5m，一质量m=0.2kg的小物块（可视为质点）放在水平轨道上的A点，A与B相距L=10m，物块与水平轨道间的动摩擦因数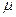
=0.1。现用一水平恒力F向右推物块，已知F=3N，当物块运动到C点时撤去该力，设C点到A点的距离为x。在圆轨道的最高点D处安装一压力传感器，当物块运动到D点时传感器就会显示相应的读数FN，压力传感器所能承受的最大压力为90N，g取10m/s2。
（1）要使物块能够安全通过圆轨道的最高点D，求x的范围；
（2）在满足（1）问的情况下，在坐标系中作出压力传感器的读数FN与x的关系图象。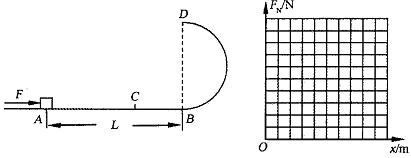
2007年10月24日，“嫦娥一号”探月卫星发射升空，实现了中华民族千年奔月的梦想。 2007年10月31日，“嫦娥一号”探月卫星在近地点600km处通过发动机短时点火，实施变轨。变轨后卫星从远地点高度12万余公里的椭圆轨道进入远地点高度37万余公里的椭圆轨道，直接奔向月球。已知地球质量大约是月球质量的8l倍，地球半径大约是月球半径的4倍，地球的第一宇宙速度是7. 9km/s。
（1）“嫦娥一号”奔向月球的过程中，“嫦娥一号”探月卫星通过月、地之间的某一位置时，月球和地球对它的引力大小相等，该位置到月球中心与到地球中心的距离之比是多少？
（2）如果在月球表面发射月球的卫星，求卫星的第一宇宙速度是多少。
2009年1月5日上午，中航一集团研制的歼—10战斗机正式亮相。歼—10战斗机是我国自主研制的第三代多用途战斗机。假设歼—10战斗机的质量为4.0×l03Kg，起飞过程中从静止开始滑跑，当位移达到2.0×102m耐达到起飞速度100 m/s，在此过程中飞机受到的平均阻力是飞机重量的0.02倍。g取10m/s2。求
（1）飞机受到的平均阻力多大？
（2）飞机受到的牵引力多大？