(本小题满分10分)
某食品公司为了解某种新品种食品的市场需求，进行了20天的测试，人为地调控每天产品的单价P(元/件)：前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表：
| 时间(将第x天记为x) x |
1 |
10 |
11 |
18 |
| 单价(元/件)P |
9 |
0 |
1 |
8 |
而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.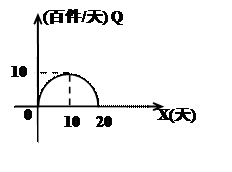
(1)写出每天销售y(元)与时间x(天)的函数关系式y=f(x);
(2)在这20天中哪一天销售收入最高？为使每天销售收入最高,按此测试结果应将单价P设定为多少元为好?(结果精确到1元)
已知函数，
(l)求函数
的最小正周期；
(2)当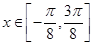
时，求函数f(x)的单调区间。
已知函数
(1)若函数
的图象切x轴于点(2，0)，求a、b的值；
(2)设函数
的图象上任意一点的切线斜率为k，试求
的充要条件；
(3)若函数的图象上任意不同的两点的连线的斜率小于l，求证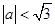
．
给定椭圆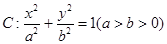
．称圆心在原点O，半径为
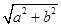的圆是椭圆C的“准圆”．若椭圆C的一个焦点为
，其短轴上的一个端点到F的距离为
．
(1)求椭圆C的方程和其“准圆”方程；
(2)点P是椭圆C的“准圆”上的一个动点，过动点P作直线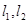
，使得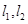
与椭圆C都只有一个交点，试判断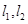是否垂直？并说明理由．
已知函数
， 数列
满足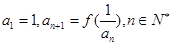
．
(1)求数列的通项公式；
(2)令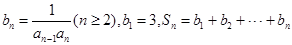
，若
对一切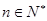
成立，求最小正整数m．
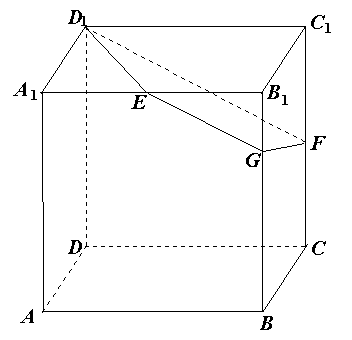
如图，已知正方体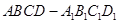
的棱长为2，E、F分别是
、
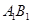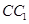的中点，过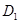
、E、F作平面
交
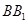于G．
(l)求证：EG∥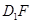
；
(2)求二面角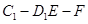
的余弦值；
(3)求正方体被平面所截得的几何体
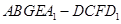的体积．